


Next: Transformation of Laplace Tidal
Up: Terrestrial Ocean Tides
Previous: Non-Global Ocean Tides
Let
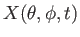 ,
,
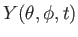 ,
,
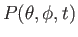 , and
, and
 be well-behaved functions of
be well-behaved functions of 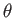 and
and 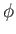 .
Suppose that
.
Suppose that
![$\displaystyle D\,P = -\frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,X) +\frac{\partial Y}{\partial\phi}\right],$](img4732.png) |
(12.186) |
where
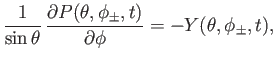 |
(12.187) |
Suppose, further, that
![$\displaystyle D\,Q =\frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,Y) - \frac{\partial X}{\partial\phi}\right],$](img4734.png) |
(12.188) |
where
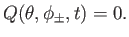 |
(12.189) |
We wish to demonstrate that
Let
Note, from Equations (12.192) and (12.194), that
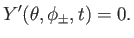 |
(12.194) |
It follows from Equations (12.191), (12.193), (12.197), and (12.198) that
Equations (12.199) and (12.201) imply that
and
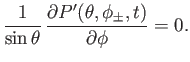 |
(12.199) |
Furthermore, Equation (12.200) yields
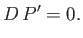 |
(12.200) |
Multiplying by  , integrating over the ocean, and making use of the boundary condition (12.204),
we obtain
, integrating over the ocean, and making use of the boundary condition (12.204),
we obtain
![$\displaystyle \int_{\mit\Omega}\left[\left(\frac{\partial P'}{\partial\theta}\r...
...}{\sin\theta}\,\frac{\partial P'}{\partial\phi}\right)^2\right]d{\mit\Omega}=0.$](img4749.png) |
(12.201) |
Here,
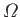 is the surface of the Earth that is covered by ocean, and
is the surface of the Earth that is covered by ocean, and
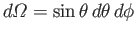 .
It follows that
.
It follows that  is a constant.
Thus, Equations (12.202) and (12.203) imply that
is a constant.
Thus, Equations (12.202) and (12.203) imply that 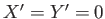 , and, hence, that Equations (12.195) and (12.196)
are valid.
, and, hence, that Equations (12.195) and (12.196)
are valid.



Next: Transformation of Laplace Tidal
Up: Terrestrial Ocean Tides
Previous: Non-Global Ocean Tides
Richard Fitzpatrick
2016-01-22
![$\displaystyle D\,P = -\frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,X) +\frac{\partial Y}{\partial\phi}\right],$](img4732.png)
![$\displaystyle \int_{\mit\Omega}\left[\left(\frac{\partial P'}{\partial\theta}\r...
...}{\sin\theta}\,\frac{\partial P'}{\partial\phi}\right)^2\right]d{\mit\Omega}=0.$](img4749.png)