


Next: Gravity Waves in Shallow
Up: Waves in Incompressible Fluids
Previous: Gravity Waves
Gravity Waves in Deep Water
Consider the so-called deep water limit,
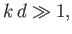 |
(11.22) |
in which the depth, 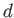 , of the water greatly exceeds the wavelength,
, of the water greatly exceeds the wavelength,
 , of the wave.
In this limit, the gravity wave dispersion relation (11.21) reduces to
, of the wave.
In this limit, the gravity wave dispersion relation (11.21) reduces to
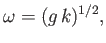 |
(11.23) |
because
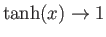 as
as
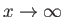 . It follows that the phase velocity of gravity waves in deep water is
. It follows that the phase velocity of gravity waves in deep water is
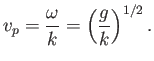 |
(11.24) |
Note that this velocity is proportional to the square root of the wavelength. Hence, deep-water gravity waves with long wavelengths propagate faster
than those with short wavelengths. The phase velocity,
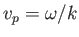 , is defined as the propagation velocity of a
plane wave with the definite wave number,
, is defined as the propagation velocity of a
plane wave with the definite wave number, 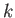 [and a frequency given by the dispersion relation (11.23)] (Fitzpatrick 2013). Such a wave has an infinite spatial extent. A more realistic wave of finite spatial extent,
with an approximate wave number
[and a frequency given by the dispersion relation (11.23)] (Fitzpatrick 2013). Such a wave has an infinite spatial extent. A more realistic wave of finite spatial extent,
with an approximate wave number 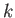 , can be formed as a linear superposition of plane waves
having a range of different wave numbers centered on
, can be formed as a linear superposition of plane waves
having a range of different wave numbers centered on 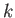 . Such a construct is known as a wave pulse (Fitzpatrick 2013).
As is well known, wave pulses propagate at the group velocity (Fitzpatrick 2013),
. Such a construct is known as a wave pulse (Fitzpatrick 2013).
As is well known, wave pulses propagate at the group velocity (Fitzpatrick 2013),
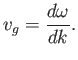 |
(11.25) |
For the case of gravity waves in deep water, the dispersion relation (11.23) yields
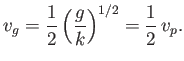 |
(11.26) |
In other words, the group velocity of such waves is half their phase velocity.
Let
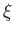
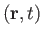 be the displacement of a particle of water, found at position
be the displacement of a particle of water, found at position  and time
and time 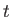 , due to the passage of a
deep water gravity wave. It follows that
, due to the passage of a
deep water gravity wave. It follows that
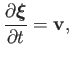 |
(11.27) |
where
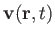 is the perturbed velocity. For a plane wave of wave number
is the perturbed velocity. For a plane wave of wave number
 , in the limit
, in the limit  ,
Equation (11.19) yields
,
Equation (11.19) yields
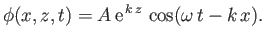 |
(11.28) |
Hence, [cf., Equations (11.45)-(11.48)]
and
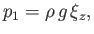 |
(11.33) |
where use has been made of Equations (11.7), (11.9), and (11.27).
Here, 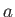 is the amplitude of the vertical oscillation at the water's surface. According to
Equations (11.29)-(11.32), the passage of the wave causes a water particle located a depth
is the amplitude of the vertical oscillation at the water's surface. According to
Equations (11.29)-(11.32), the passage of the wave causes a water particle located a depth  below the surface to execute a
circular orbit of radius
below the surface to execute a
circular orbit of radius
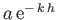 about its equilibrium position. The radius of the orbit
decreases exponentially with increasing depth. Furthermore, whenever the particle's vertical displacement attains a maximum value the
particle is
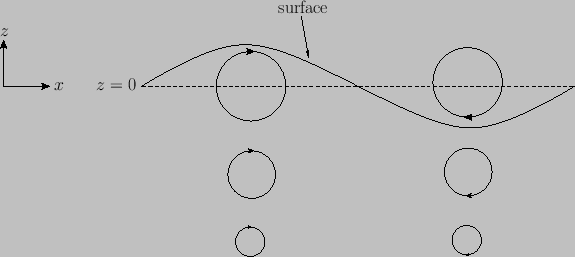
moving horizontally in the same direction as the wave, and vice versa. (See Figure 11.1.)
about its equilibrium position. The radius of the orbit
decreases exponentially with increasing depth. Furthermore, whenever the particle's vertical displacement attains a maximum value the
particle is
moving horizontally in the same direction as the wave, and vice versa. (See Figure 11.1.)
Figure:
Motion of water particles associated with a deep water gravity wave propagating in the  -direction.
-direction.
 |
Finally, if we define
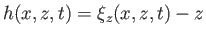 as the equilibrium depth of the water particle found at a given point and time then
Equations (11.3) and (11.33) yield
as the equilibrium depth of the water particle found at a given point and time then
Equations (11.3) and (11.33) yield
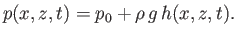 |
(11.34) |
In other words, the pressure at this point and time is the same as the unperturbed pressure calculated at the equilibrium depth of the
water particle.



Next: Gravity Waves in Shallow
Up: Waves in Incompressible Fluids
Previous: Gravity Waves
Richard Fitzpatrick
2016-01-22
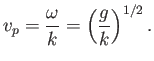
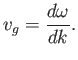
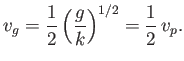
![]()
![]() be the displacement of a particle of water, found at position
be the displacement of a particle of water, found at position ![]() and time
and time ![]() , due to the passage of a
deep water gravity wave. It follows that
, due to the passage of a
deep water gravity wave. It follows that

![]() as the equilibrium depth of the water particle found at a given point and time then
Equations (11.3) and (11.33) yield
as the equilibrium depth of the water particle found at a given point and time then
Equations (11.3) and (11.33) yield