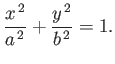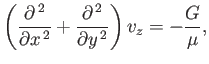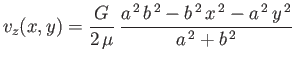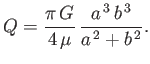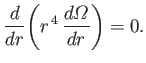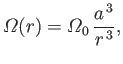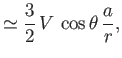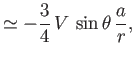Next: Waves in Incompressible Fluids
Up: Incompressible Viscous Flow
Previous: Axisymmetric Stokes Flow In
- Consider viscous fluid flow down a plane that is inclined at an angle
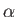 to the horizontal. Let
to the horizontal. Let  measure distance
along the plane (i.e., along the path of steepest decent), and let
measure distance
along the plane (i.e., along the path of steepest decent), and let  be a transverse coordinate such that the surface of the plane
corresponds to
be a transverse coordinate such that the surface of the plane
corresponds to 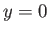 , and the free surface of the fluid to
, and the free surface of the fluid to 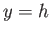 . Show that within the fluid (i.e.,
. Show that within the fluid (i.e.,
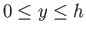 )
)
where 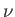 is the kinematic viscosity,
is the kinematic viscosity, 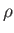 the density, and
the density, and 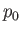 is atmospheric pressure.
is atmospheric pressure.
- If a viscous fluid flows along a cylindrical pipe of circular cross-section that is inclined at an angle
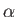 to the horizontal show that
the flow rate is
to the horizontal show that
the flow rate is
where 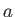 is the pipe radius,
is the pipe radius, 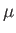 the fluid viscosity,
the fluid viscosity, 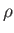 the fluid density, and
the fluid density, and 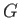 the pressure gradient.
the pressure gradient.
- Viscous fluid flows steadily, parallel to the axis, in the annular region between two coaxial cylinders of radii
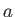 and
and 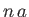 , where
, where 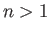 .
Show that the volume flux of fluid flow is
.
Show that the volume flux of fluid flow is
where 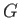 is the effective pressure gradient, and
is the effective pressure gradient, and 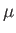 the viscosity. Find the mean flow speed.
the viscosity. Find the mean flow speed.
- Consider viscous flow along a cylindrical pipe of elliptic cross-section. Suppose that the pipe runs parallel to the
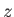 -axis, and that its
boundary satisfies
-axis, and that its
boundary satisfies
Let
Demonstrate that
where 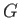 is the effective pressure gradient, and
is the effective pressure gradient, and 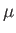 the fluid viscosity. Show that
the fluid viscosity. Show that
is a solution of this equation that satisfies the no slip condition at the boundary. Demonstrate that the
flow rate is
Finally, show that a pipe with an elliptic cross-section has lower flow rate than an otherwise similar pipe of circular cross-section that has the
same cross-sectional area.
- Consider a velocity field of the form
where 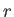 ,
, 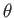 ,
, 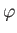 are spherical coordinates. Demonstrate that this field satisfies the equations of
steady, incompressible, viscous fluid flow (neglecting advective inertia) with uniform pressure (neglecting gravity)
provided that
are spherical coordinates. Demonstrate that this field satisfies the equations of
steady, incompressible, viscous fluid flow (neglecting advective inertia) with uniform pressure (neglecting gravity)
provided that
Suppose that a solid sphere of radius 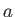 , centered at the origin, is rotating about the
, centered at the origin, is rotating about the 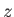 -axis, at the uniform
angular velocity
-axis, at the uniform
angular velocity
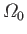 , in a viscous fluid, of viscosity
, in a viscous fluid, of viscosity 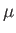 , that is stationary at infinity. Demonstrate that
, that is stationary at infinity. Demonstrate that
for 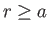 . Show that the torque that the sphere exerts on the fluid is
. Show that the torque that the sphere exerts on the fluid is
- Consider a solid sphere of radius
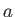 moving through a viscous fluid of viscosity
moving through a viscous fluid of viscosity 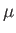 at the fixed velocity
at the fixed velocity
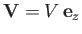 .
Let
.
Let 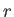 ,
, 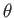 ,
, 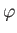 be spherical coordinates whose origin coincides with the instantaneous location of the sphere's center. Show that,
if inertia and gravity are negligible, the fluid velocity, and the radial components of the stress tensor, a long way from the sphere, are
be spherical coordinates whose origin coincides with the instantaneous location of the sphere's center. Show that,
if inertia and gravity are negligible, the fluid velocity, and the radial components of the stress tensor, a long way from the sphere, are
respectively. Hence, deduce that the net force exerted on the fluid lying inside a large spherical surface of radius 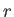 , by the fluid external to the
surface, is
, by the fluid external to the
surface, is
independent of the surface radius.



Next: Waves in Incompressible Fluids
Up: Incompressible Viscous Flow
Previous: Axisymmetric Stokes Flow In
Richard Fitzpatrick
2016-01-22
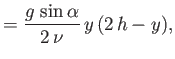
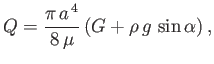
![$\displaystyle Q = \frac{\pi\,G\,a^{\,4}}{8\,\mu}\left[n^4-1 - \frac{(n^2-1)^2}{\ln n}\right],
$](img3874.png)