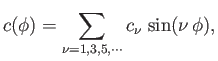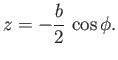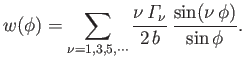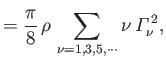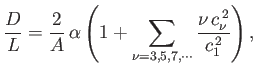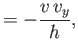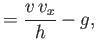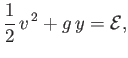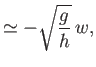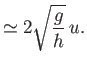Next: Incompressible Viscous Flow
Up: Incompressible Aerodynamics
Previous: Simple Flight Problems
- Consider the integral
where 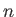 is a non-negative integer. This integral is defined by its Cauchy principal value
is a non-negative integer. This integral is defined by its Cauchy principal value
As was demonstrated in Section 9.9,
Show that
and
and, hence, that
- Suppose that an airfoil of negligible thickness, and wingspan
 , has a width whose
, has a width whose  variation is expressed parametrically
as
variation is expressed parametrically
as
for
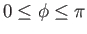 , where
, where
Show that the air circulation about the airfoil takes the form
where
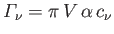 . Here,
. Here, 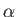 is the angle of attack (which is assumed to
be small).
Demonstrate that the downwash velocity at the trailing edge of the airfoil is
is the angle of attack (which is assumed to
be small).
Demonstrate that the downwash velocity at the trailing edge of the airfoil is
Hence, show that the lift and induced drag acting on the airfoil take the values
respectively.
Demonstrate that the drag to lift ratio can be written
where 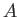 is the aspect ratio.
Hence, deduce that the airfoil shape (in the
is the aspect ratio.
Hence, deduce that the airfoil shape (in the  -
- ) plane that minimizes this ratio (at fixed aspect ratio) is an ellipse (i.e., such
that
) plane that minimizes this ratio (at fixed aspect ratio) is an ellipse (i.e., such
that 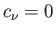 for
for 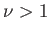 ).
).
- Consider a plane that flies with a constant angle of attack, and whose thrust is adjusted such that it cancels the induced
drag. The plane is effectively subject to two forces. First, its weight,
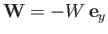 , and
second its lift
, and
second its lift
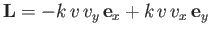 . Here,
. Here,  and
and  are horizontal and
vertical coordinates, respectively,
are horizontal and
vertical coordinates, respectively,  is the plane's instantaneous velocity, and
is the plane's instantaneous velocity, and 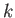 is a positive constant. Note that the lift is directed at right angles to the
plane's instantaneous direction of motion, and has a magnitude proportional to the square of its airspeed. Demonstrate that the
plane's equations of motion can be written
is a positive constant. Note that the lift is directed at right angles to the
plane's instantaneous direction of motion, and has a magnitude proportional to the square of its airspeed. Demonstrate that the
plane's equations of motion can be written
where 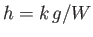 is a positive constant with the dimensions of length. Show that
is a positive constant with the dimensions of length. Show that
where  is a constant. Suppose that
is a constant. Suppose that
 and
and
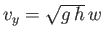 , where
, where 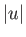 ,
, 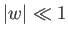 .
Demonstrate that, to first order in perturbed quantities,
.
Demonstrate that, to first order in perturbed quantities,
Hence, deduce that if the plane is flying horizontally at some speed 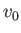 , and is subject to a small perturbation, then its altitude oscillates
sinusoidally at the angular frequency
, and is subject to a small perturbation, then its altitude oscillates
sinusoidally at the angular frequency
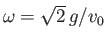 . This type of oscillation is known as a phugoid oscillation.
. This type of oscillation is known as a phugoid oscillation.



Next: Incompressible Viscous Flow
Up: Incompressible Aerodynamics
Previous: Simple Flight Problems
Richard Fitzpatrick
2016-01-22
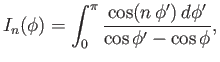
![$\displaystyle I_n(\phi)=\lim_{\epsilon\rightarrow 0}\left[ \int_0^{\phi-\epsilo...
..._{\phi+\epsilon}^\pi \frac{\cos(n\,\phi')\,d\phi'}{\cos\phi'-\cos\phi}\right].
$](img3539.png)