


Next: Ellipsoidal Airfoils
Up: Incompressible Aerodynamics
Previous: Three-Dimensional Airfoils
Aerodynamic Forces
The net aerodynamic force acting on an three-dimensional airfoil of finite size can be written
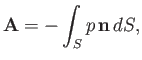 |
(9.70) |
where the integral is taken over the surface of the airfoil,  . Here,
. Here, 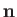 is an outward unit normal vector on
is an outward unit normal vector on  ,
, 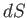 is an element of
is an element of  , and
, and 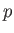 is the air pressure. From Bernoulli's theorem (in an irrotational fluid), we can write
is the air pressure. From Bernoulli's theorem (in an irrotational fluid), we can write
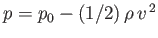 , where
, where 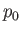 is
a constant pressure. Because a constant pressure exerts no net force on a closed surface, we get
is
a constant pressure. Because a constant pressure exerts no net force on a closed surface, we get
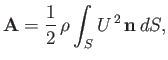 |
(9.71) |
where 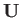 is the tangential air velocity just above the surface of the airfoil. Now,
is the tangential air velocity just above the surface of the airfoil. Now,
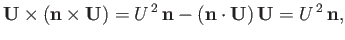 |
(9.72) |
because
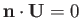 on the surface. Hence,
on the surface. Hence,
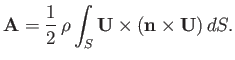 |
(9.73) |
Making use of Equations (9.64) and (9.69), the previous expression can be written
where
Here,  ,
,
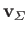 , and
, and 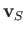 are the incident wind velocity, the velocity induced by the free vortices in the wake,
and the velocity induced by the bound
vortices covering the surface of the airfoil, respectively. The forces
are the incident wind velocity, the velocity induced by the free vortices in the wake,
and the velocity induced by the bound
vortices covering the surface of the airfoil, respectively. The forces 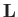 and
and 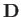 are called the lift and the induced drag, respectively. (Note, that
are called the lift and the induced drag, respectively. (Note, that 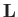 now represents a net force, rather than a force
per unit length.) We shall presently demonstrate that the force
now represents a net force, rather than a force
per unit length.) We shall presently demonstrate that the force 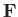 is negligible.
is negligible.
Let us assume that
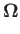  |
(9.78) |
that is, that the bound vortices covering the surface of the
airfoil run parallel to the  -axis. This assumption is exactly correct for an airfoil of infinite wingspan
and constant cross-section. Moreover, it is a good approximation for an airfoil of finite wingspan, provided the airfoil's length greatly exceeds
its width (i.e.,
-axis. This assumption is exactly correct for an airfoil of infinite wingspan
and constant cross-section. Moreover, it is a good approximation for an airfoil of finite wingspan, provided the airfoil's length greatly exceeds
its width (i.e., 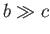 ). Now, the incident wind velocity is written
). Now, the incident wind velocity is written
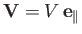 .
Moreover,
.
Moreover,
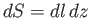 , where
, where 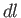 is an element of length that runs parallel to the
is an element of length that runs parallel to the  -
- plane whilst lying on the airfoil surface.
Making use of the curl theorem, we can easily show that
plane whilst lying on the airfoil surface.
Making use of the curl theorem, we can easily show that
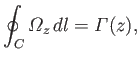 |
(9.79) |
where the closed curve 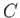 is the intersection of the airfoil surface with the plane
is the intersection of the airfoil surface with the plane  , and
, and
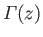 is the
air circulation about the airfoil in this plane. Thus, it follows from Equation (9.75) that
is the
air circulation about the airfoil in this plane. Thus, it follows from Equation (9.75) that
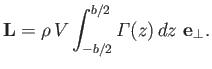 |
(9.80) |
This expression is the generalization of Equation (9.31) for a three-dimensional airfoil of finite size. As before, the lift
is at right-angles to the incident wind direction.
Let us make the further assumption--known as the lifting line approximation (because the lifting action of the wing is effectively concentrated
onto a line)--that
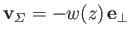 |
(9.81) |
throughout  ,
where
,
where
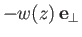 is the induced velocity due to the free vortices in
is the induced velocity due to the free vortices in
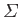 , evaluated at the trailing edge of the airfoil.
Here, the velocity
, evaluated at the trailing edge of the airfoil.
Here, the velocity 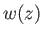 is called the downwash velocity. It follows from Equation (9.76) that
is called the downwash velocity. It follows from Equation (9.76) that
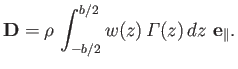 |
(9.82) |
Note that the induced drag is parallel to the incident wind direction. The origin of induced drag is as follows. It takes energy to constantly
resupply free vortices to the wake, as they are swept downstream by the wind (note that a vortex filament possesses energy by virtue of the kinetic energy of its induced flow pattern), and
this energy is supplied by the work done in opposing the induced drag. The drag acting on a well-designed airfoil (i.e., an airfoil with an aerodynamic shape that
minimizes form drag) situated in a high Reynolds number wind (which implies that the friction drag is negligible) is generally dominated
by induced drag.
According to Equations (9.62) and (9.77), the force 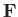 is written
is written
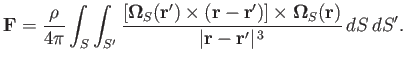 |
(9.83) |
We can interchange primed and unprimed variables without changing the value of the integral. Hence,
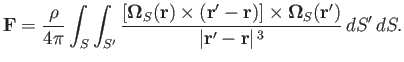 |
(9.84) |
Taking the half the sum of the previous two equations, we obtain
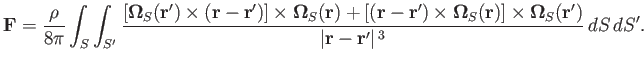 |
(9.85) |
However,
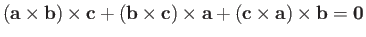 . Thus,
the previous expression yields
. Thus,
the previous expression yields
![$\displaystyle {\bf F} = \frac{\rho}{8\pi}\int_S\int_{S'}\frac{[\mbox{\boldmath$...
...{\bf r})]\times ({\bf r}-{\bf r}')}{\vert{\bf r}-{\bf r}'\vert^{\,3}}\,dS\,dS'.$](img3461.png) |
(9.86) |
But, the assumption (9.78) implies that
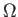
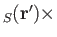
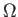
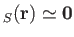 . Hence,
. Hence, 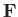 is negligible, as
was previously stated.
is negligible, as
was previously stated.
Consider a closed surface covering the small section of the airfoil lying between the parallel planes  and
and  . The flux of vorticity into the surface due to bound vortices
at
. The flux of vorticity into the surface due to bound vortices
at  is
is
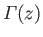 . The flux of vorticity out of the surface due to bound vortices at
. The flux of vorticity out of the surface due to bound vortices at 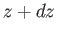 is
is
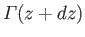 .
Finally, the flux of vorticity out of the surface due to the free vortices in the part of the wake lying between
.
Finally, the flux of vorticity out of the surface due to the free vortices in the part of the wake lying between  and
and 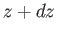 is
is 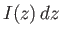 . However, the net flux of vorticity out of a closed surface is zero, because vorticity is divergence free.
Hence,
. However, the net flux of vorticity out of a closed surface is zero, because vorticity is divergence free.
Hence,
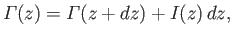 |
(9.87) |
which implies that
 |
(9.88) |
Figure 9.12:
Semi-infinite vortex filament.
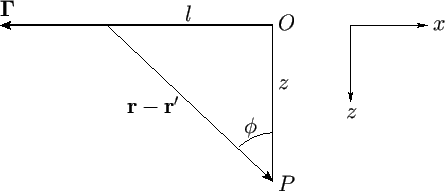 |
Finally, consider a semi-infinite straight vortex filament of vortex intensity
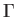
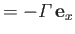 that terminates
at the origin,
that terminates
at the origin, 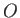 , as shown in Figure 9.12. Let us calculate the flow velocity induced by this filament
at the point
, as shown in Figure 9.12. Let us calculate the flow velocity induced by this filament
at the point
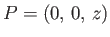 . From the diagram
. From the diagram
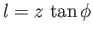 ,
,
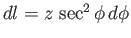 ,
,
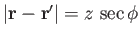 , and
, and
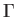
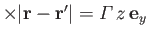 . Hence, from Equation (9.61), the induced
velocity at
. Hence, from Equation (9.61), the induced
velocity at 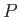 is
is
 , where
, where
 |
(9.89) |
This result allows us to calculate the downwash velocity,
 , induced at the trailing edge of the airfoil by the semi-infinite free vortices in the wake.
The vortex intensity in the small section of the wake lying between
, induced at the trailing edge of the airfoil by the semi-infinite free vortices in the wake.
The vortex intensity in the small section of the wake lying between  and
and 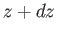 is
is 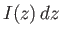 , so we obtain
, so we obtain
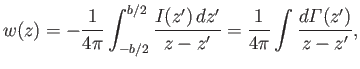 |
(9.90) |
where use has been made of Equation (9.88).



Next: Ellipsoidal Airfoils
Up: Incompressible Aerodynamics
Previous: Three-Dimensional Airfoils
Richard Fitzpatrick
2016-01-22
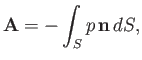
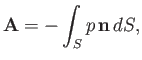
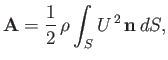
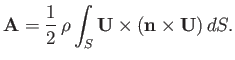
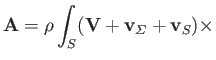
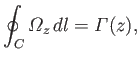
![]() is written
is written
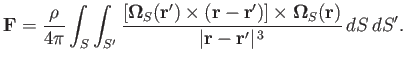
![$\displaystyle {\bf F} = \frac{\rho}{8\pi}\int_S\int_{S'}\frac{[\mbox{\boldmath$...
...{\bf r})]\times ({\bf r}-{\bf r}')}{\vert{\bf r}-{\bf r}'\vert^{\,3}}\,dS\,dS'.$](img3461.png)
![]() and
and ![]() . The flux of vorticity into the surface due to bound vortices
at
. The flux of vorticity into the surface due to bound vortices
at ![]() is
is
![]() . The flux of vorticity out of the surface due to bound vortices at
. The flux of vorticity out of the surface due to bound vortices at ![]() is
is
![]() .
Finally, the flux of vorticity out of the surface due to the free vortices in the part of the wake lying between
.
Finally, the flux of vorticity out of the surface due to the free vortices in the part of the wake lying between ![]() and
and ![]() is
is ![]() . However, the net flux of vorticity out of a closed surface is zero, because vorticity is divergence free.
Hence,
. However, the net flux of vorticity out of a closed surface is zero, because vorticity is divergence free.
Hence,
![]()
![]() that terminates
at the origin,
that terminates
at the origin, ![]() , as shown in Figure 9.12. Let us calculate the flow velocity induced by this filament
at the point
, as shown in Figure 9.12. Let us calculate the flow velocity induced by this filament
at the point
![]() . From the diagram
. From the diagram
![]() ,
,
![]() ,
,
![]() , and
, and
![]()
![]() . Hence, from Equation (9.61), the induced
velocity at
. Hence, from Equation (9.61), the induced
velocity at ![]() is
is
![]() , where
, where
