Next: Navier-Stokes Equation
Up: Mathematical Models of Fluid
Previous: Convective Time Derivative
Momentum Conservation
Consider a fixed volume  surrounded by a surface
surrounded by a surface  . The
. The  -component of the total linear momentum contained within
-component of the total linear momentum contained within  is
is
 |
(1.43) |
Moreover, the flux of  -momentum across
-momentum across  , and out of
, and out of  , is [see Equation (1.29)]
, is [see Equation (1.29)]
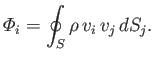 |
(1.44) |
Finally, the 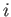 -component of the net force acting on the fluid within
-component of the net force acting on the fluid within  is
is
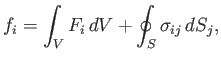 |
(1.45) |
where the first and second terms on the right-hand side are the contributions from volume and surface forces, respectively.
Momentum conservation requires that the rate of
increase of the net 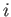 -momentum of the fluid contained within
-momentum of the fluid contained within  , plus the flux of
, plus the flux of 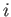 -momentum out of
-momentum out of  , is equal to the rate of
, is equal to the rate of 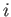 -momentum generation
within
-momentum generation
within  . Of course, from Newton's second law of motion, the latter quantity is equal to the
. Of course, from Newton's second law of motion, the latter quantity is equal to the 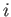 -component
of the net force acting on the fluid contained within
-component
of the net force acting on the fluid contained within  . Thus, we obtain [cf., Equation (1.31)]
. Thus, we obtain [cf., Equation (1.31)]
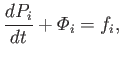 |
(1.46) |
which can be written
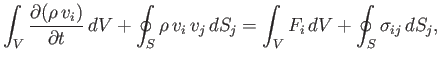 |
(1.47) |
because the volume  is non-time-varying.
Making use of the tensor divergence theorem, this becomes
is non-time-varying.
Making use of the tensor divergence theorem, this becomes
![$\displaystyle \int_V\left[\frac{\partial (\rho\,v_i)}{\partial t} + \frac{\part...
...right]dV = \int_V\left(F_i + \frac{\partial\sigma_{ij}}{\partial x_j}\right)dV.$](img273.png) |
(1.48) |
However, the previous result is valid irrespective of the size, shape, or location of volume  , which is only
possible if
, which is only
possible if
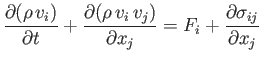 |
(1.49) |
everywhere inside the fluid. Expanding the derivatives, and rearranging, we obtain
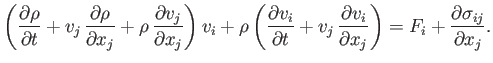 |
(1.50) |
In tensor notation, the continuity equation (1.37) is written
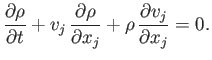 |
(1.51) |
So, combining Equations (1.50) and (1.51), we obtain the following fluid equation of motion,
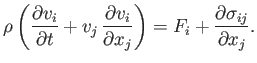 |
(1.52) |
An alternative form of this equation is
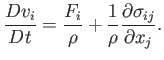 |
(1.53) |
The previous equation describes how the net volume and surface forces per unit mass acting on a co-moving fluid element determine its acceleration.



Next: Navier-Stokes Equation
Up: Mathematical Models of Fluid
Previous: Convective Time Derivative
Richard Fitzpatrick
2016-01-22


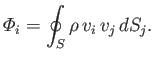
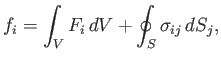
![]() -momentum of the fluid contained within
-momentum of the fluid contained within ![]() , plus the flux of
, plus the flux of ![]() -momentum out of
-momentum out of ![]() , is equal to the rate of
, is equal to the rate of ![]() -momentum generation
within
-momentum generation
within ![]() . Of course, from Newton's second law of motion, the latter quantity is equal to the
. Of course, from Newton's second law of motion, the latter quantity is equal to the ![]() -component
of the net force acting on the fluid contained within
-component
of the net force acting on the fluid contained within ![]() . Thus, we obtain [cf., Equation (1.31)]
. Thus, we obtain [cf., Equation (1.31)]
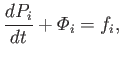
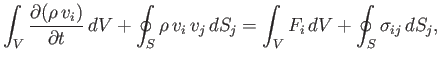
![$\displaystyle \int_V\left[\frac{\partial (\rho\,v_i)}{\partial t} + \frac{\part...
...right]dV = \int_V\left(F_i + \frac{\partial\sigma_{ij}}{\partial x_j}\right)dV.$](img273.png)