


Next: Solution of electron equations
Up: Particle-in-cell codes
Previous: Introduction
It is convenient to normalize time with respect to 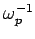 , where
, where
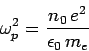 |
(294) |
is the so-called plasma frequency: i.e., the typical frequency of electrostatic electron oscillations. Likewise it is convenient to normalize length with respect to the so-called Debye length:
which is the length-scale above which the electrons exhibit collective (i.e.,
plasma-like) effects, instead of acting like individual particles.
Our normalized equations take the form:
whereas our initial distribution function becomes
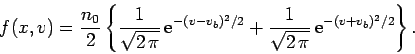 |
(299) |
Note that 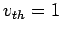 in normalized units.
in normalized units.
Let us solve the above system of equations in the domain 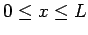 .
Furthermore, for the sake of simplicity, let us adopt periodic boundary conditions:
i.e., let us identify the left and right boundaries of our solution domain.
It follows that
.
Furthermore, for the sake of simplicity, let us adopt periodic boundary conditions:
i.e., let us identify the left and right boundaries of our solution domain.
It follows that 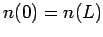 ,
,
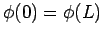 , and
, and 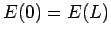 . Moreover, any electron
which crosses the right boundary of the solution domain must reappear at the left boundary with
the same velocity, and
vice versa.
. Moreover, any electron
which crosses the right boundary of the solution domain must reappear at the left boundary with
the same velocity, and
vice versa.



Next: Solution of electron equations
Up: Particle-in-cell codes
Previous: Introduction
Richard Fitzpatrick
2006-03-29
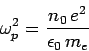
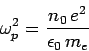
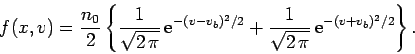
![]() .
Furthermore, for the sake of simplicity, let us adopt periodic boundary conditions:
i.e., let us identify the left and right boundaries of our solution domain.
It follows that
.
Furthermore, for the sake of simplicity, let us adopt periodic boundary conditions:
i.e., let us identify the left and right boundaries of our solution domain.
It follows that ![]() ,
,
![]() , and
, and ![]() . Moreover, any electron
which crosses the right boundary of the solution domain must reappear at the left boundary with
the same velocity, and
vice versa.
. Moreover, any electron
which crosses the right boundary of the solution domain must reappear at the left boundary with
the same velocity, and
vice versa.