


Next: The physics of baseball
Up: Integration of ODEs
Previous: An example adaptive-step RK4
Of course, Runge-Kutta methods are not the last word in integrating o.d.e.s. Far from
it! Runge-Kutta methods are sometimes referred to as single-step methods,
since they evolve the solution from 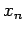 to
to 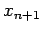 without needing to
know the solutions at
without needing to
know the solutions at 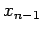 ,
, 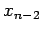 , etc. There is a broad
class of more sophisticated integration methods, known as multi-step methods,
which utilize the previously calculated solutions at
, etc. There is a broad
class of more sophisticated integration methods, known as multi-step methods,
which utilize the previously calculated solutions at 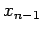 ,
, 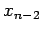 ,
etc. in order to evolve the solution from
,
etc. in order to evolve the solution from 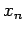 to
to 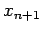 . Examples of these
methods are the various Adams methods17 and the various Predictor-Corrector
methods.18 The main advantages of
Runge-Kutta methods are that they are easy to implement, they are very stable,
and they are ``self-starting'' (i.e., unlike muti-step methods, we do not
have to treat the first few steps taken by a single-step integration method as special cases).
The primary disadvantages of Runge-Kutta methods are that they require significantly
more computer time than multi-step methods of comparable accuracy, and
they do not easily yield good global estimates of the truncation error. However, for the straightforward
dynamical systems under investigation in this course, the advantage of the relative simplicity and
ease of use of Runge-Kutta methods far outweighs the disadvantage of their
relatively high computational cost.
. Examples of these
methods are the various Adams methods17 and the various Predictor-Corrector
methods.18 The main advantages of
Runge-Kutta methods are that they are easy to implement, they are very stable,
and they are ``self-starting'' (i.e., unlike muti-step methods, we do not
have to treat the first few steps taken by a single-step integration method as special cases).
The primary disadvantages of Runge-Kutta methods are that they require significantly
more computer time than multi-step methods of comparable accuracy, and
they do not easily yield good global estimates of the truncation error. However, for the straightforward
dynamical systems under investigation in this course, the advantage of the relative simplicity and
ease of use of Runge-Kutta methods far outweighs the disadvantage of their
relatively high computational cost.



Next: The physics of baseball
Up: Integration of ODEs
Previous: An example adaptive-step RK4
Richard Fitzpatrick
2006-03-29