


Next: Monte-Carlo integration
Up: Monte-Carlo methods
Previous: Random numbers
Let 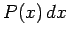 represent the probability of finding the random variable
represent the probability of finding the random variable 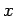 in the
interval
in the
interval 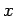 to
to 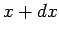 . Here,
. Here, 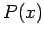 is termed a probability density. Note that
is termed a probability density. Note that
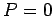 corresponds to no chance, whereas
corresponds to no chance, whereas 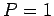 corresponds to certainty. Since
it is certain that the value of
corresponds to certainty. Since
it is certain that the value of 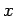 lies in the range
lies in the range 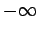 to
to 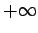 ,
probability densities are subject to the normalizing constraint
,
probability densities are subject to the normalizing constraint
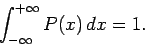 |
(315) |
Suppose that we wish to construct a random variable 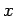 which is uniformly
distributed in the range
which is uniformly
distributed in the range 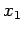 to
to 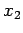 . In other words, the probability
density of
. In other words, the probability
density of 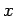 is
is
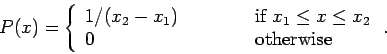 |
(316) |
Such a variable is constructed as follows
x = x1 + (x2 - x1) * double (random ()) / double (RANDMAX);
There are two basic methods of constructing non-uniformly distributed random variables:
i.e., the transformation method and the rejection method. We shall examine
each of these methods in turn.
Let us first consider the transformation method. Let 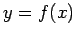 , where
, where 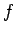 is a known function, and
is a known function, and
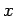 is a random variable. Suppose that
the probability density of
is a random variable. Suppose that
the probability density of 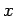 is
is 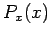 . What is the probability density,
. What is the probability density, 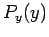 , of
, of  ?
Our basic rule is the conservation of probability:
?
Our basic rule is the conservation of probability:
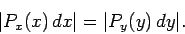 |
(317) |
In other words, the probability of finding 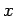 in the interval
in the interval 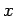 to
to 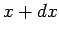 is the
same as the probability of finding
is the
same as the probability of finding  in the interval
in the interval  to
to 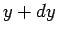 . It follows
that
. It follows
that
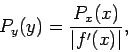 |
(318) |
where 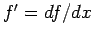 .
.
For example, consider the Poisson distribution:
 |
(319) |
Let 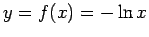 , so that
, so that 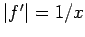 . Suppose that
. Suppose that
 |
(320) |
It follows that
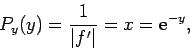 |
(321) |
with 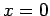 corresponding to
corresponding to 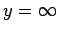 , and
, and 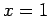 corresponding to
corresponding to 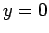 . We conclude that
if
. We conclude that
if
x = double (random ()) / double (RANDMAX);
y = - log (x);
then y is distributed according to the Poisson distribution.
The transformation method requires a differentiable probability distribution function. This is
not always practical. In such cases, we can use the rejection method instead.
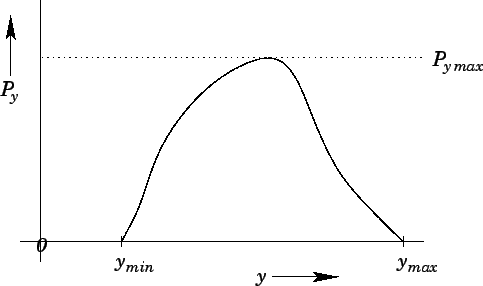
Suppose that we desire a random variable  distributed with density
distributed with density 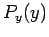 in the
range
in the
range 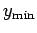 to
to 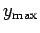 . Let
. Let
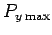 be the maximum value of
be the maximum value of 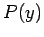 in this range (see
Fig. 95).
The rejection method is as follows. The variable
in this range (see
Fig. 95).
The rejection method is as follows. The variable  is sampled randomly in the range
is sampled randomly in the range 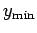 to
to 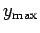 .
For each value of
.
For each value of  we first evaluate
we first evaluate 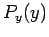 . We next generate a random number
. We next generate a random number 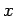 which is
uniformly distributed in the range 0 to
which is
uniformly distributed in the range 0 to
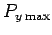 . Finally, if
. Finally, if 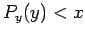 then we reject
the
then we reject
the  value; otherwise, we keep it. If this prescription is followed then
value; otherwise, we keep it. If this prescription is followed then  will
be distributed according to
will
be distributed according to 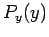 .
.
Figure 95:
The rejection method.
 |
As an example, consider the Gaussian distribution:
![\begin{displaymath}
P_y(y) =\frac{{\rm exp}[(y-\bar{y})^2/2\,\sigma^2]}{\sqrt{2\pi}\,\sigma},
\end{displaymath}](img1211.png) |
(322) |
where 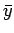 is the mean value of
is the mean value of  , and
, and 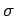 is the standard deviation.
Let
is the standard deviation.
Let
since there is a negligible chance that  lies more than 4 standard deviations
from its mean value.
It follows that
lies more than 4 standard deviations
from its mean value.
It follows that
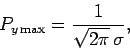 |
(325) |
with the maximum occurring at 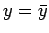 .
The function listed below employs the rejection method to return a
random variable distributed according to a Gaussian distribution
with mean mean and standard deviation sigma:
.
The function listed below employs the rejection method to return a
random variable distributed according to a Gaussian distribution
with mean mean and standard deviation sigma:
// gaussian.cpp
// Function to return random variable distributed
// according to Gaussian distribution with mean mean
// and standard deviation sigma.
#define RANDMAX 2147483646
int random (int = 0);
double gaussian (double mean, double sigma)
{
double ymin = mean - 4. * sigma;
double ymax = mean + 4. * sigma;
double Pymax = 1. / sqrt (2. * M_PI) / sigma;
// Calculate random value uniformly distributed
// in range ymin to ymax
double y = ymin + (ymax - ymin) * double (random ()) / double (RANDMAX);
// Calculate Py
double Py = exp (- (y - mean) * (y - mean) / 2. / sigma / sigma) /
sqrt (2. * M_PI) / sigma;
// Calculate random value uniformly distributed in range 0 to Pymax
double x = Pymax * double (random ()) / double (RANDMAX);
// If x > Py reject value and recalculate
if (x > Py) return gaussian (mean, sigma);
else return y;
}
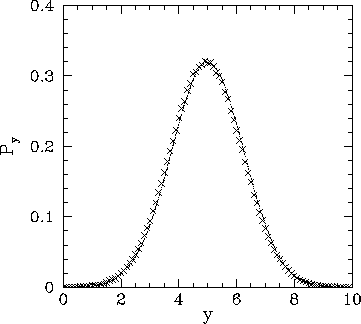
Figure 96 illustrates the performance of the above function. It can be seen
that the function successfully returns a random value distributed according to the Gaussian distribution.
Figure:
A million values returned by function gaussian with
mean = 5. and sigma = 1.25. The values are binned
in 100 bins of width 0.1. The figure shows the number of points
in each bin divided by a suitable normalization factor. A Gaussian curve
is shown for comparison.
 |



Next: Monte-Carlo integration
Up: Monte-Carlo methods
Previous: Random numbers
Richard Fitzpatrick
2006-03-29
![]() which is uniformly
distributed in the range
which is uniformly
distributed in the range ![]() to
to ![]() . In other words, the probability
density of
. In other words, the probability
density of ![]() is
is
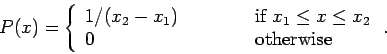
![]() , where
, where ![]() is a known function, and
is a known function, and
![]() is a random variable. Suppose that
the probability density of
is a random variable. Suppose that
the probability density of ![]() is
is ![]() . What is the probability density,
. What is the probability density, ![]() , of
, of ![]() ?
Our basic rule is the conservation of probability:
?
Our basic rule is the conservation of probability:
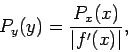


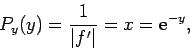
![]() distributed with density
distributed with density ![]() in the
range
in the
range ![]() to
to ![]() . Let
. Let
![]() be the maximum value of
be the maximum value of ![]() in this range (see
Fig. 95).
The rejection method is as follows. The variable
in this range (see
Fig. 95).
The rejection method is as follows. The variable ![]() is sampled randomly in the range
is sampled randomly in the range ![]() to
to ![]() .
For each value of
.
For each value of ![]() we first evaluate
we first evaluate ![]() . We next generate a random number
. We next generate a random number ![]() which is
uniformly distributed in the range 0 to
which is
uniformly distributed in the range 0 to
![]() . Finally, if
. Finally, if ![]() then we reject
the
then we reject
the ![]() value; otherwise, we keep it. If this prescription is followed then
value; otherwise, we keep it. If this prescription is followed then ![]() will
be distributed according to
will
be distributed according to ![]() .
.
![\begin{displaymath}
P_y(y) =\frac{{\rm exp}[(y-\bar{y})^2/2\,\sigma^2]}{\sqrt{2\pi}\,\sigma},
\end{displaymath}](img1211.png)
