


Next: Emf and Internal Resistance
Up: Electric Current
Previous: Ohm's Law
Resistance and Resistivity
Let us attempt to find a microscopic explanation for electrical
resistance and Ohm's law. Now, electric current in metals, and most other conductors found
in conventional electric circuits (good or bad), is carried by free electrons.
Consider a uniform wire of cross-sectional area  and length
and length  made of some
conducting material. Suppose that the potential difference between
the two ends of the wire is
made of some
conducting material. Suppose that the potential difference between
the two ends of the wire is 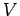 . The longitudinal electric field inside
the wire is therefore
. The longitudinal electric field inside
the wire is therefore 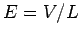 . Consider a free electron
of charge
. Consider a free electron
of charge 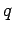 and mass
and mass  inside the
wire. The electric field in the wire exerts a force
inside the
wire. The electric field in the wire exerts a force  on the electron, causing
it to accelerate with an acceleration
on the electron, causing
it to accelerate with an acceleration 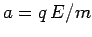 along the direction of
the wire. However, the electron does not accelerate for ever. Eventually,
it crashes into one of the atoms in the wire. Since atoms are far more massive
than electrons, the electron loses all forward momentum every time it hits
an atom (just as we would lose all forward momentum if we ran into a brick wall).
Suppose that the average time interval between
collisions is
along the direction of
the wire. However, the electron does not accelerate for ever. Eventually,
it crashes into one of the atoms in the wire. Since atoms are far more massive
than electrons, the electron loses all forward momentum every time it hits
an atom (just as we would lose all forward momentum if we ran into a brick wall).
Suppose that the average time interval between
collisions is 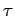 . Of course, this
characteristic time interval depends on the size and number density of the atoms
in the wire.
Immediately after the electron hits an atom (at
. Of course, this
characteristic time interval depends on the size and number density of the atoms
in the wire.
Immediately after the electron hits an atom (at  , say) its forward velocity
, say) its forward velocity 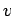 is
zero. The electron is then accelerated by the electric
field, so
is
zero. The electron is then accelerated by the electric
field, so
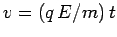 . The final velocity of the electron is
. The final velocity of the electron is
 , and its average velocity is
, and its average velocity is
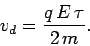 |
(128) |
In fact, on average, the electron acts as though it drifts along the
wire with the constant velocity 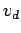 . This velocity
is therefore called the drift velocity.
. This velocity
is therefore called the drift velocity.
Suppose that there are 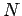 free electrons per unit volume in the wire. All
of these electrons effectively drift along the wire with the drift velocity
free electrons per unit volume in the wire. All
of these electrons effectively drift along the wire with the drift velocity 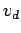 .
Thus, the total charge which passes any particular point on the wire in
a time interval
.
Thus, the total charge which passes any particular point on the wire in
a time interval  is
is
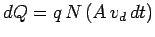 .
This follows because all free electrons contained in a tube of
length
.
This follows because all free electrons contained in a tube of
length 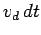 and cross-sectional area
and cross-sectional area  pass the point in
question in the time interval
pass the point in
question in the time interval  .
The electric current
.
The electric current  flowing in the wire is given by
flowing in the wire is given by
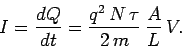 |
(129) |
This equation can be rearranged to give Ohm's law,
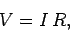 |
(130) |
where
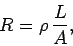 |
(131) |
and
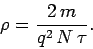 |
(132) |
Thus, we can indeed account for Ohm's law on a microscopic level.
According to Eq. (131), the resistance of a wire is proportional
to its length, and inversely proportional to its cross-sectional area.
The constant of proportionality 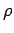 is called the resistivity of the material making
up the wire. The units of resistivity are ohm-meters (
is called the resistivity of the material making
up the wire. The units of resistivity are ohm-meters (
 ). Table 2
below shows the resistivities of some common metals at
). Table 2
below shows the resistivities of some common metals at 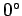 C.
C.
Table 2:
Resistivities of some common metals at 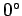 C.
C.
| Material |
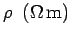 |
| Silver |
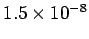 |
| Copper |
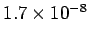 |
| Aluminium |
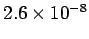 |
| Iron |
 |
|



Next: Emf and Internal Resistance
Up: Electric Current
Previous: Ohm's Law
Richard Fitzpatrick
2007-07-14
![]() free electrons per unit volume in the wire. All
of these electrons effectively drift along the wire with the drift velocity
free electrons per unit volume in the wire. All
of these electrons effectively drift along the wire with the drift velocity ![]() .
Thus, the total charge which passes any particular point on the wire in
a time interval
.
Thus, the total charge which passes any particular point on the wire in
a time interval ![]() is
is
![]() .
This follows because all free electrons contained in a tube of
length
.
This follows because all free electrons contained in a tube of
length ![]() and cross-sectional area
and cross-sectional area ![]() pass the point in
question in the time interval
pass the point in
question in the time interval ![]() .
The electric current
.
The electric current ![]() flowing in the wire is given by
flowing in the wire is given by