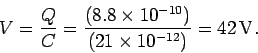Next: Example 6.3: Equivalent capacitance
Up: Capacitance
Previous: Example 6.1: Parallel plate
Question:
A parallel plate capacitor has a plate area of
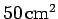 and a plate
separation of
and a plate
separation of 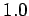 cm. A potential difference of
cm. A potential difference of  V is applied
across the plates with no dielectric present. The battery is then disconnected,
and a piece of Bakelite (
V is applied
across the plates with no dielectric present. The battery is then disconnected,
and a piece of Bakelite ( ) is inserted which fills the region between
the plates. What is the capacitance, the charge on the plates, and the
potential difference between the plates, before and after the dielectric
is inserted?
) is inserted which fills the region between
the plates. What is the capacitance, the charge on the plates, and the
potential difference between the plates, before and after the dielectric
is inserted?
Answer: Before the dielectric is inserted,
the space between the plates is presumably filled
with air. Since the dielectric constant of air is virtually
indistinguishable from that of a vacuum, let us use the vacuum formula (108) to
calculate the initial capacitance 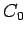 . Thus,
. Thus,
After the dielectric is inserted, the capacitance increases by a factor 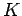 ,
which in this case is
,
which in this case is 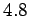 , so the new capacitance
, so the new capacitance 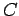 is given by
is given by
Before the dielectric is inserted, the charge 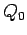 on the plates is
simply
on the plates is
simply
After the dielectric is inserted, the charge 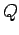 is exactly the same, since the
capacitor is disconnected, and so the charge cannot leave the plates.
Hence,
is exactly the same, since the
capacitor is disconnected, and so the charge cannot leave the plates.
Hence,
The potential difference before the dielectric is inserted is given as
 V. The potential difference
V. The potential difference 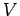 after the dielectric is
inserted is simply
after the dielectric is
inserted is simply
Note, of course, that 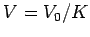 .
.



Next: Example 6.3: Equivalent capacitance
Up: Capacitance
Previous: Example 6.1: Parallel plate
Richard Fitzpatrick
2007-07-14
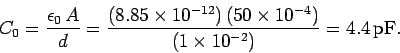
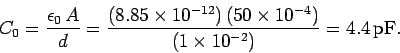
![]() on the plates is
simply
on the plates is
simply
![]() V. The potential difference
V. The potential difference ![]() after the dielectric is
inserted is simply
after the dielectric is
inserted is simply