The phenomenon of breakdown sets an upper limit on the charge which
can be stored on a conductor. There is, however, another important factor which
affects the onset of breakdown. This is best illustrated in the following
simple example. Suppose that we have two charged conducting spheres of radii ![]() and
and
![]() , respectively, which are connected by a long conducting wire. The wire allows charge to
move back and forth between the spheres until they reach the same potential (recall
that the electric potential is uniform in a conductor). Let
, respectively, which are connected by a long conducting wire. The wire allows charge to
move back and forth between the spheres until they reach the same potential (recall
that the electric potential is uniform in a conductor). Let ![]() be the
charge on the first sphere, and
be the
charge on the first sphere, and ![]() the charge on the second sphere. Of course,
the total charge
the charge on the second sphere. Of course,
the total charge
![]() carried by the two spheres is a conserved quantity.
The electric field generated by each sphere is the same as if the charge on that
sphere were concentrated at its centre. Assuming that the wire is sufficiently
long that the two spheres do not
affect one another very much, the absolute potential of the first sphere
is
carried by the two spheres is a conserved quantity.
The electric field generated by each sphere is the same as if the charge on that
sphere were concentrated at its centre. Assuming that the wire is sufficiently
long that the two spheres do not
affect one another very much, the absolute potential of the first sphere
is
![]() , whereas that of the second
sphere is
, whereas that of the second
sphere is
![]() [see Eq. (97)]. Since
[see Eq. (97)]. Since ![]() , we find that
, we find that
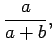 |
(101) | ||
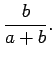 |
(102) |
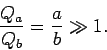 |
(103) |
Equation (104) is a special case of a far more general rule: i.e., the electric field-strength above some point on the surface of a conductor is inversely proportional to the local radius of curvature of the surface. It is clear that if we wish to store significant amounts of charge on a conductor then the surface of the conductor must be made as smooth as possible. Any sharp spikes on the surface possess relatively small radii of curvature. Intense local electric fields are generated above these spikes whenever the conductor is charged. These fields can easily exceed the critical field for the breakdown of air, leading to sparking, and the eventual loss of the charge on the conductor. Sparking tends to be very destructive because of its highly localized nature, which leads inevitably to very large electric currents, and, hence, to intense heating.
Clouds can acquire very large negative charges during thunderstorms. An equal and opposite positive charge is induced on the surface of the Earth. The electric field generated between the clouds and the Earth can become sufficiently large to cause breakdown in the atmosphere, giving rise to the phenomenon which we call lightning. Let us consider the various factors which determine where lightning strikes. Breakdown starts at cloud level, as a so-called ``dark leader'' of ionized air traces out a path towards the ground. When it comes within about 10 meters of ground level, a second dark leader comes up from the ground to meet it. Once the two leaders meet, and a conducting path is established, the lightning strike proper occurs. Note that, contrary to popular opinion, the lightning strike travels upwards from the Earth to the clouds. It is clear that lightning ``strikes'' a particular object on the ground because the object emits a dark leader: i.e., because breakdown takes place just above the object. In a thunderstorm, the ground, and the objects upon it, acts essentially like a charged conductor with a convoluted surface. Thus, any ``spikes'' on the ground (e.g., a person standing in a field, a radio mast, a lightning rod) are comparatively more likely to be hit by lightning, because the electric field-strength above these points is relatively large, which facilitates breakdown.