Charged Conductors

Suppose that we put a negative charge on an arbitrarily shaped, solid, conducting object. Where does the excess negative charge end up after the charges have attained their equilibrium positions?

Let us construct a gaussian surface which lies just inside the surface of the conductor. Application of Gauss' law yields

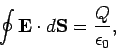$$\oint {\bf E}\cdot d{\bf S} = \frac{Q}{\epsilon_0},$$ (75)

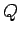where $Q$ is the enclosed charge. But, the electric field-strength inside a conductor must be zero, since the charges are free to move through the conductor, and will, thus, continue to move until no field remains. Hence, the left-hand side of the above equation is zero, and, therefore, the right-hand side must also be zero. This can only be the case if there are no charges enclosed by the gaussian surface. In other words, there can be no excess charge in the interior of the conductor. Instead, all of the excess charge must be distributed over the surface of the conductor. It follows that:

Any excess charge on a solid conductor resides entirely on the outer surface of the conductor.