


Next: Example 3.3: Electric field
Up: Electricity
Previous: Example 3.1: Electrostatic force between
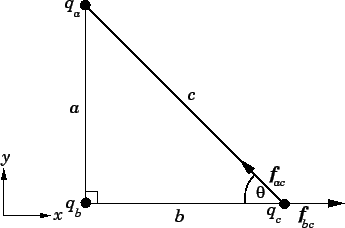
Question: Suppose that three point charges, 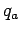 ,
, 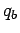 , and
, and 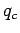 , are arranged at the
vertices of a right-angled triangle, as shown in the diagram. What is the magnitude and
direction of the electrostatic force acting on the third charge if
, are arranged at the
vertices of a right-angled triangle, as shown in the diagram. What is the magnitude and
direction of the electrostatic force acting on the third charge if
 ,
,
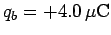 ,
,
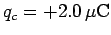 ,
,
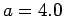 m, and
m, and 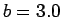 m?
m?
Solution: The magnitude 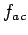 of the force
of the force 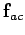 exerted
by charge
exerted
by charge 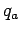 on charge
on charge 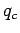 is given by
is given by
where use has been made of the Pythagorean theorem.
The force is attractive (since charges 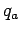 and
and 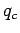 are of opposite sign). Hence,
the force is directed from charge
are of opposite sign). Hence,
the force is directed from charge 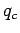 towards charge
towards charge 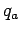 , as shown in the diagram.
The magnitude
, as shown in the diagram.
The magnitude 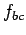 of the force
of the force 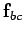 exerted
by charge
exerted
by charge 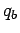 on charge
on charge 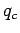 is given by
is given by
The force is repulsive (since charges 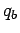 and
and 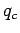 are of the same sign). Hence,
the force is directed from charge
are of the same sign). Hence,
the force is directed from charge 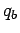 towards charge
towards charge 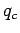 , as shown in the diagram.
Now, the net force acting on charge
, as shown in the diagram.
Now, the net force acting on charge 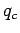 is the sum of
is the sum of 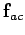 and
and 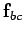 .
Unfortunately, since
.
Unfortunately, since 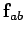 and
and 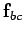 are vectors pointing in different
directions, they cannot be added together algebraically. Fortunately, however,
their components along the
are vectors pointing in different
directions, they cannot be added together algebraically. Fortunately, however,
their components along the 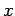 - and
- and 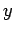 -axes can be added algebraically.
Now, it is clear, from the diagram, that
-axes can be added algebraically.
Now, it is clear, from the diagram, that 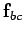 is directed along the
is directed along the
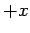 -axis. If follows that
-axis. If follows that
It is also clear, from the diagram, that 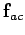 subtends an angle
subtends an angle
with the 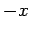 -axis, and an angle
-axis, and an angle
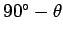 with the
with the 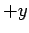 -axis.
It follows from the conventional laws of vector projection that
-axis.
It follows from the conventional laws of vector projection that
The 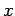 - and
- and 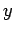 -components of the resultant force
-components of the resultant force 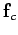 acting on charge
acting on charge 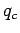 are given by
are given by
Thus, from the Pythagorean theorem, the magnitude of the resultant force is
Furthermore, the resultant force subtends an
angle
with the 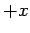 -axis, and an angle
-axis, and an angle
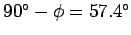 with the
with the 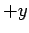 -axis.
-axis.



Next: Example 3.3: Electric field
Up: Electricity
Previous: Example 3.1: Electrostatic force between
Richard Fitzpatrick
2007-07-14

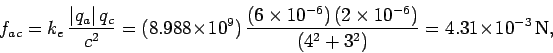

![]() - and
- and ![]() -components of the resultant force
-components of the resultant force ![]() acting on charge
acting on charge ![]() are given by
are given by