


Next: Electric Fields
Up: Electricity
Previous: Induced Electric Charge
The first precise measurement of the force between two electric charges was
performed by the French scientist Charles-Augustin de Coulomb in 1788. Coulomb concluded that:
The electrical force between two
charges at rest is directly proportional to the product of the charges, and
inversely proportional to the square of the distance between the charges
This law of force is nowadays known as Coulomb's law.
Incidentally, an electrical force exerted between two stationary charges
is known as an electrostatic force.
In algebraic
form, Coulomb's law is written
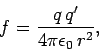 |
(54) |
where 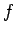 is the magnitude of the
force,
is the magnitude of the
force, 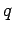 and
and 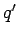 are the magnitudes of the two charges
(with the appropriate signs), and
are the magnitudes of the two charges
(with the appropriate signs), and  is the distance between the two charges.
The force is repulsive if
is the distance between the two charges.
The force is repulsive if 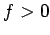 , and attractive if
, and attractive if 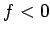 .
The universal constant
.
The universal constant
 |
(55) |
is called the permittivity of free space or the permittivity
of the vacuum. We can also write Coulomb's law in the form
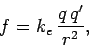 |
(56) |
where the constant of proportionality
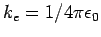 takes the value
takes the value
 |
(57) |
Coulomb's law has an analogous form to Newton's law of gravitation,
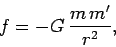 |
(58) |
with
electric charge playing the role of mass. One major difference
between the two laws is the sign of the force.
The electrostatic force between two
like charges is repulsive (i.e., 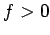 ), whereas that between two
unlike charges is attractive (i.e.,
), whereas that between two
unlike charges is attractive (i.e., 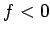 ). On the other hand, the
gravitational force between two masses is always attractive (since there is
no such thing as a negative mass). Another major difference is the relative magnitude
of the two forces. For instance, the electrostatic repulsion between two electrons is
approximately
). On the other hand, the
gravitational force between two masses is always attractive (since there is
no such thing as a negative mass). Another major difference is the relative magnitude
of the two forces. For instance, the electrostatic repulsion between two electrons is
approximately 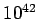 times larger than the corresponding
gravitational attraction.
times larger than the corresponding
gravitational attraction.
The electrostatic force 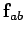 exerted by a charge
exerted by a charge 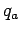 on a second charge
on a second charge 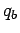 , located
a distance
, located
a distance  from the first charge, has the magnitude
from the first charge, has the magnitude
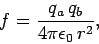 |
(59) |
and is directed radially away from the first charge if 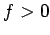 , and radially
towards it if
, and radially
towards it if 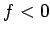 . The force
. The force
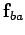 exerted by the second charge
on the first is equal and opposite to
exerted by the second charge
on the first is equal and opposite to 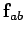 ,
so that
,
so that
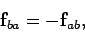 |
(60) |
in accordance with Newton's
third law of motion.
Suppose that we have three point charges, 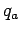 ,
, 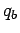 , and
, and 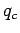 .
It turns out that electrostatic
forces are superposable. That is, the force
.
It turns out that electrostatic
forces are superposable. That is, the force 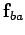 exerted by
exerted by
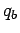 on
on 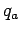 is completely unaffected by the presence of
is completely unaffected by the presence of 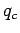 . Likewise, the
force
. Likewise, the
force 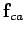 exerted by
exerted by 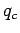 on
on 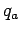 is unaffected by the presence of
is unaffected by the presence of 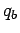 .
Thus, the net force
.
Thus, the net force 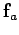 acting on
acting on 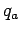 is the resultant of these two
forces: i.e.,
is the resultant of these two
forces: i.e.,
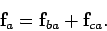 |
(61) |
This rule can be generalized in a straightforward manner
to the case where there are more than three point
charges.



Next: Electric Fields
Up: Electricity
Previous: Induced Electric Charge
Richard Fitzpatrick
2007-07-14
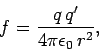
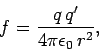
![]() exerted by a charge
exerted by a charge ![]() on a second charge
on a second charge ![]() , located
a distance
, located
a distance ![]() from the first charge, has the magnitude
from the first charge, has the magnitude
![]() ,
, ![]() , and
, and ![]() .
It turns out that electrostatic
forces are superposable. That is, the force
.
It turns out that electrostatic
forces are superposable. That is, the force ![]() exerted by
exerted by
![]() on
on ![]() is completely unaffected by the presence of
is completely unaffected by the presence of ![]() . Likewise, the
force
. Likewise, the
force ![]() exerted by
exerted by ![]() on
on ![]() is unaffected by the presence of
is unaffected by the presence of ![]() .
Thus, the net force
.
Thus, the net force ![]() acting on
acting on ![]() is the resultant of these two
forces: i.e.,
is the resultant of these two
forces: i.e.,