


Next: Example 13.3: Converging lenses
Up: Paraxial Optics
Previous: Example 13.1: Concave mirrors
Question: How far must an object be
placed in front of a convex mirror
of radius of curvature 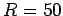 cm in order to ensure that the
size of the image is ten times less than the
size of the object? How far behind the
mirror is the image located?
cm in order to ensure that the
size of the image is ten times less than the
size of the object? How far behind the
mirror is the image located?
Answer: The focal length 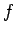 of a convex mirror is minus
half of its radius of curvature (taking the sign convention for
the focal lengths of convex mirrors into account). Thus,
of a convex mirror is minus
half of its radius of curvature (taking the sign convention for
the focal lengths of convex mirrors into account). Thus, 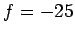 cm.
If the image is ten times smaller than the object then the magnification
is
cm.
If the image is ten times smaller than the object then the magnification
is
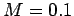 . We can be sure that
. We can be sure that 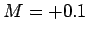 , as opposed to
, as opposed to  , because
we know that images formed in convex mirrors are always virtual and
upright.
According to Eq. (352), the image distance
, because
we know that images formed in convex mirrors are always virtual and
upright.
According to Eq. (352), the image distance 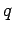 is given by
is given by
where 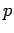 is the object distance. This can be combined with Eq. (358)
to give
is the object distance. This can be combined with Eq. (358)
to give
Thus, the object must be placed 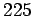 cm in front of the mirror.
The image distance is given by
cm in front of the mirror.
The image distance is given by
Thus, the image is located 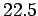 cm behind the mirror.
cm behind the mirror.



Next: Example 13.3: Converging lenses
Up: Paraxial Optics
Previous: Example 13.1: Concave mirrors
Richard Fitzpatrick
2007-07-14