 |
Let us now introduce a few key concepts which are needed to
study image formation by a concave spherical mirror.
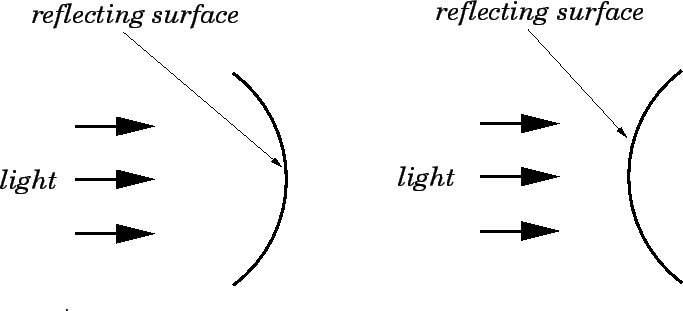
As illustrated in Fig. 69, the normal to the centre of
the mirror is called the principal axis.
The mirror is assumed to be rotationally symmetric about
this axis. Hence, we can represent a three-dimensional
mirror in a two-dimensional diagram, without loss of generality.
The point ![]() at which the principal axis touches the surface of the
mirror is called the vertex. The point
at which the principal axis touches the surface of the
mirror is called the vertex. The point ![]() , on the principal
axis, which is equidistant from all points on the reflecting
surface of the mirror is called the centre of curvature.
The distance along the principal axis from point
, on the principal
axis, which is equidistant from all points on the reflecting
surface of the mirror is called the centre of curvature.
The distance along the principal axis from point ![]() to point
to point ![]() is called the radius of curvature of the mirror,
and is denoted
is called the radius of curvature of the mirror,
and is denoted ![]() . It is found experimentally that rays striking a
concave mirror parallel to its principal axis, and not too far away
from this axis, are reflected by the mirror such that they all pass
through the same point
. It is found experimentally that rays striking a
concave mirror parallel to its principal axis, and not too far away
from this axis, are reflected by the mirror such that they all pass
through the same point ![]() on the principal axis. This
point, which is lies between the centre of curvature and the vertex, is
called the focal point, or focus, of the mirror.
The distance along the principal axis from the focus to the
vertex is called the focal length of the mirror, and is
denoted
on the principal axis. This
point, which is lies between the centre of curvature and the vertex, is
called the focal point, or focus, of the mirror.
The distance along the principal axis from the focus to the
vertex is called the focal length of the mirror, and is
denoted ![]() .
.
In our study of concave mirrors, we are going to
assume that all light-rays which strike
a mirror parallel to its principal axis (e.g., all rays
emanating from a distant object) are brought to a focus at the same
point ![]() .
Of course, as mentioned above, this is only an approximation.
It turns out that as rays from a distant object depart further
from the principal axis of a concave mirror they are brought
to a focus ever closer to the mirror, as shown in Fig. 70. This
lack of perfect focusing of a spherical mirror is called
spherical aberration. The approximation in which
we neglect spherical aberration is called the paraxial
approximation.3 Likewise, the study of image formation under this approximation
is known as paraxial optics. This
field of optics was first investigated systematically by
the famous German mathematician
Karl Friedrich Gauss in 1841.
.
Of course, as mentioned above, this is only an approximation.
It turns out that as rays from a distant object depart further
from the principal axis of a concave mirror they are brought
to a focus ever closer to the mirror, as shown in Fig. 70. This
lack of perfect focusing of a spherical mirror is called
spherical aberration. The approximation in which
we neglect spherical aberration is called the paraxial
approximation.3 Likewise, the study of image formation under this approximation
is known as paraxial optics. This
field of optics was first investigated systematically by
the famous German mathematician
Karl Friedrich Gauss in 1841.
It can be demonstrated, by geometry, that the
only type of mirror which does not suffer from
spherical aberration is a parabolic mirror (i.e., a mirror
whose reflecting surface is the surface of revolution of a
parabola). Thus, a ray traveling parallel to the principal
axis of a parabolic mirror is brought to a focus at the same point ![]() ,
no matter how far the ray is from the axis. Since the path
of a light-ray is completely reversible, it follows
that a light source placed at the focus
,
no matter how far the ray is from the axis. Since the path
of a light-ray is completely reversible, it follows
that a light source placed at the focus ![]() of a parabolic
mirror yields a perfectly parallel beam of light, after the light has reflected
off the surface of the mirror. Parabolic mirrors are more
difficult, and, therefore, more expensive, to make than
spherical mirrors. Thus, parabolic mirrors are only
used in situations where the spherical aberration of
a conventional spherical mirror would be a serious problem.
The receiving dishes of radio telescopes are generally
parabolic. They reflect
the incoming radio waves from (very) distant astronomical
sources, and bring them
to a focus at a single point, where a detector is placed. In this
case, since the sources are extremely faint, it is imperative to
avoid the signal losses which would be associated with spherical
aberration. A car headlight consists of a light-bulb placed at the
focus of a parabolic reflector. The use of a parabolic reflector
enables the headlight to cast a very straight beam of light ahead of
the car. The beam would be nowhere near as well-focused were a
spherical reflector used instead.
of a parabolic
mirror yields a perfectly parallel beam of light, after the light has reflected
off the surface of the mirror. Parabolic mirrors are more
difficult, and, therefore, more expensive, to make than
spherical mirrors. Thus, parabolic mirrors are only
used in situations where the spherical aberration of
a conventional spherical mirror would be a serious problem.
The receiving dishes of radio telescopes are generally
parabolic. They reflect
the incoming radio waves from (very) distant astronomical
sources, and bring them
to a focus at a single point, where a detector is placed. In this
case, since the sources are extremely faint, it is imperative to
avoid the signal losses which would be associated with spherical
aberration. A car headlight consists of a light-bulb placed at the
focus of a parabolic reflector. The use of a parabolic reflector
enables the headlight to cast a very straight beam of light ahead of
the car. The beam would be nowhere near as well-focused were a
spherical reflector used instead.