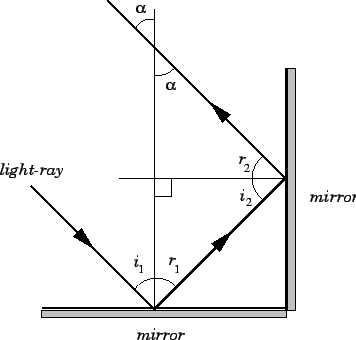

It can easily be appreciated that a combination of three
mutually perpendicular mirrors would reflect a light-ray incident from
any direction through ![]() . Such a combination of
mirrors is
called a corner-cube reflector. Astronauts on the Apollo 11
mission (1969) left a panel of
corner-cube reflectors on the surface of the Moon. These reflectors
have been used ever since to measure the Earth-Moon distance
via laser range finding (basically, a laser beam is fired from
the Earth, reflects off the corner-cube reflectors on the
Moon, and then returns to the Earth. The time of travel of the beam
can easily be converted into the Earth-Moon distance). The Earth-Moon
distance can be measured to within an accuracy of
. Such a combination of
mirrors is
called a corner-cube reflector. Astronauts on the Apollo 11
mission (1969) left a panel of
corner-cube reflectors on the surface of the Moon. These reflectors
have been used ever since to measure the Earth-Moon distance
via laser range finding (basically, a laser beam is fired from
the Earth, reflects off the corner-cube reflectors on the
Moon, and then returns to the Earth. The time of travel of the beam
can easily be converted into the Earth-Moon distance). The Earth-Moon
distance can be measured to within an accuracy of ![]() using
this method.
using
this method.