 |
The colours of a rainbow vary smoothly from red on the outside
of the arc to violet on the inside. A rainbow has a
diffuse inner edge, and a sharp outer edge.
Sometimes a secondary arc
is observed. This is fainter and larger
(with an angular radius of ![]() ) than the primary
arc, and the order of the colours is reversed (i.e., red is
on the inside, and violet on the outside). The secondary
arc has a diffuse outer edge, and a sharp inner edge. The sky between
the two arcs sometimes appears to be less bright than the sky elsewhere.
This region is called Alexander's dark band, in honour of
Alexander of Aphrodisias who described it some 1800 years ago.
) than the primary
arc, and the order of the colours is reversed (i.e., red is
on the inside, and violet on the outside). The secondary
arc has a diffuse outer edge, and a sharp inner edge. The sky between
the two arcs sometimes appears to be less bright than the sky elsewhere.
This region is called Alexander's dark band, in honour of
Alexander of Aphrodisias who described it some 1800 years ago.
Rainbows have been studied since ancient times. Aristotle wrote extensively on rainbows in his De Meteorologica,2 and even speculated that a rainbow is caused by the reflection of sunlight from the drops of water in a cloud.
The first scientific study of rainbows was performed by Theodoric, professor of theology at Freiburg, in the fourteenth century. He studied the path of a light-ray through a spherical globe of water in his laboratory, and suggested that the globe be thought of as a model of a single falling raindrop. A ray, from the Sun, entering the drop, is refracted at the air-water interface, undergoes internal reflection from the inside surface of the drop, and then leaves the drop in a backward direction, after being again refracted at the surface. Thus, looking away from the Sun, towards a cloud of raindrops, one sees an enhancement of light due to these rays. Theodoric did not explain why this enhancement is concentrated at a particular angle from the direction of the Sun's rays, or why the light is split into different colours.
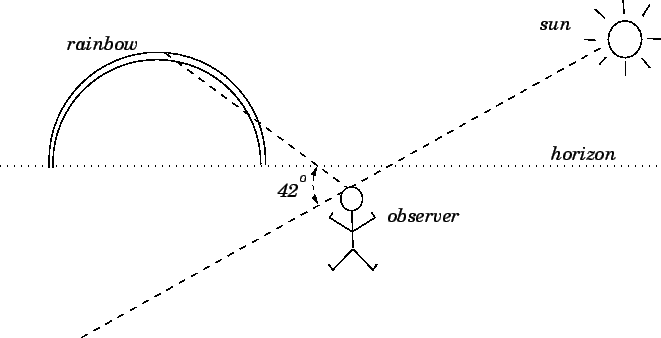
The first person to give a full explanation of how a
rainbow is formed was René Descartes. He showed mathematically
that if one traces the path through a spherical raindrop of
parallel light-rays entering the drop at different points on
its surface, each emerges in a different direction, but there
is a concentration of emerging rays at an angle of
![]() from the reverse direction to the incident rays, in exact
agreement with the observed
angular size of rainbows. Furthermore, since some colours are
refracted more than others in a
raindrop, the ``rainbow angle'' is slightly different for each
colour, so a raindrop disperses the Sun's light into a
set of nearly overlapping coloured arcs.
from the reverse direction to the incident rays, in exact
agreement with the observed
angular size of rainbows. Furthermore, since some colours are
refracted more than others in a
raindrop, the ``rainbow angle'' is slightly different for each
colour, so a raindrop disperses the Sun's light into a
set of nearly overlapping coloured arcs.
Figure 65 illustrated Descartes' theory in more detail.
It shows parallel light-rays
entering a spherical raindrop. Only
rays entering the upper half contribute to the rainbow effect. Let us
follow the rays, one by one, from the top down to the middle
of the drop. We observe the following pattern. Rays which enter near the
top of the drop emerge going in almost the reverse direction,
but a few
degrees below the horizontal. Rays entering a little
further below the top emerge at a greater angle below the horizontal.
Eventually, we reach a critical ray, called the rainbow ray, which
emerges in an angle ![]() below the horizontal. Rays
entering the drop lower than the rainbow ray emerge at an angle
less than
below the horizontal. Rays
entering the drop lower than the rainbow ray emerge at an angle
less than ![]() . Thus, the rainbow ray is the
one which
deviates
most from the reverse direction to the incident rays.
This variation, with
. Thus, the rainbow ray is the
one which
deviates
most from the reverse direction to the incident rays.
This variation, with ![]() being the maximum angle of deviation
from the reverse direction,
leads to a bunching of rays at that angle, and, hence, to an
unusually bright
arc of reflected light centred around
being the maximum angle of deviation
from the reverse direction,
leads to a bunching of rays at that angle, and, hence, to an
unusually bright
arc of reflected light centred around
![]() from the reverse direction. The arc has a sharp outer edge,
since reflected light cannot deviate by more than
from the reverse direction. The arc has a sharp outer edge,
since reflected light cannot deviate by more than ![]() from the reverse direction,
and a diffuse inner edge, since light can
deviate by less than
from the reverse direction,
and a diffuse inner edge, since light can
deviate by less than ![]() from the reverse direction:
from the reverse direction:
![]() is
just the most likely angle of deviation. Finally, since the
rainbow angle varies slightly with wavelength (because
the refractive index of water varies slightly with wavelength), the
arcs corresponding to
each colour appear at slightly different angles relative to
the reverse direction to the incident rays. We
expect violet light to be refracted more strongly than red light
in a raindrop. It is, therefore, clear, from Fig. 66,
that the red arc deviates slightly more from the reverse direction
to the incident rays than
the violet arc. In other words, violet is concentrated on the inside
of the rainbow, and red is concentrated on the outside.
is
just the most likely angle of deviation. Finally, since the
rainbow angle varies slightly with wavelength (because
the refractive index of water varies slightly with wavelength), the
arcs corresponding to
each colour appear at slightly different angles relative to
the reverse direction to the incident rays. We
expect violet light to be refracted more strongly than red light
in a raindrop. It is, therefore, clear, from Fig. 66,
that the red arc deviates slightly more from the reverse direction
to the incident rays than
the violet arc. In other words, violet is concentrated on the inside
of the rainbow, and red is concentrated on the outside.
Descartes was also able to show that light-rays which are
internally reflected
twice inside a raindrop emerge concentrated at an
angle of ![]() from the reverse direction to the incident
rays. Of course,
this angle corresponds exactly to the angular size of the secondary
rainbow sometimes seen outside the first. This rainbow
is naturally less intense than the primary rainbow, since a
light-ray loses some of its intensity at each reflection
or refraction event. Note that
from the reverse direction to the incident
rays. Of course,
this angle corresponds exactly to the angular size of the secondary
rainbow sometimes seen outside the first. This rainbow
is naturally less intense than the primary rainbow, since a
light-ray loses some of its intensity at each reflection
or refraction event. Note that ![]() represents the
angle of maximum deviation of doubly reflected light
from the reverse direction (i.e., doubly reflected
light can deviate by more than this angle, but not by less). Thus,
we expect the secondary rainbow to have a diffuse outer edge, and
a sharp inner edge. We also expect doubly reflected violet light to be
refracted more strongly in a raindrop than
doubly reflected red light. It follows, from Fig. 67,
that the red secondary arc deviates slightly less
from the reverse direction to the incident
rays than the violet secondary arc.
In other words, red is concentrated on the inside of the
secondary rainbow, and violet on the outside.
Since no reflected light emerges between the primary and secondary
rainbows (i.e., in the angular range
represents the
angle of maximum deviation of doubly reflected light
from the reverse direction (i.e., doubly reflected
light can deviate by more than this angle, but not by less). Thus,
we expect the secondary rainbow to have a diffuse outer edge, and
a sharp inner edge. We also expect doubly reflected violet light to be
refracted more strongly in a raindrop than
doubly reflected red light. It follows, from Fig. 67,
that the red secondary arc deviates slightly less
from the reverse direction to the incident
rays than the violet secondary arc.
In other words, red is concentrated on the inside of the
secondary rainbow, and violet on the outside.
Since no reflected light emerges between the primary and secondary
rainbows (i.e., in the angular range ![]() to
to ![]() ,
relative to the reverse direction),
we naturally expect this region of the sky to look
slightly less bright than the other surrounding regions of the sky,
which explains Alexander's dark band.
,
relative to the reverse direction),
we naturally expect this region of the sky to look
slightly less bright than the other surrounding regions of the sky,
which explains Alexander's dark band.