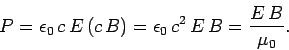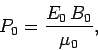Next: Worked Examples
Up: Electromagnetic Waves
Previous: Effect of Dielectric Materials
From Sect. 233, the energy stored per unit volume in an electromagnetic
wave is given by
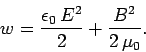 |
(331) |
Since,  , for an electromagnetic wave, and
, for an electromagnetic wave, and
 ,
the above expression yields
,
the above expression yields
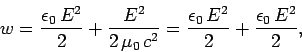 |
(332) |
or
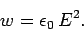 |
(333) |
It is clear, from the above, that half the energy in an
electromagnetic wave is carried by the electric field, and the other half
is carried by the magnetic field.
As an electromagnetic field propagates it transports energy. Let  be the
power per unit area carried by an electromagnetic wave:
i.e.,
be the
power per unit area carried by an electromagnetic wave:
i.e.,  is the energy transported per unit time
across a unit cross-sectional area perpendicular to the
direction in which the wave is traveling. Consider a
plane electromagnetic
wave propagating along the
is the energy transported per unit time
across a unit cross-sectional area perpendicular to the
direction in which the wave is traveling. Consider a
plane electromagnetic
wave propagating along the 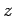 -axis. The wave propagates
a distance
-axis. The wave propagates
a distance 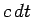 along the
along the 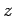 -axis in a time interval
-axis in a time interval  . If we
consider a cross-sectional area
. If we
consider a cross-sectional area  at right-angles to the
at right-angles to the 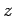 -axis, then in
a time
-axis, then in
a time  the wave sweeps through a volume
the wave sweeps through a volume 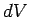 of
space, where
of
space, where
 . The
amount of energy filling this volume is
. The
amount of energy filling this volume is
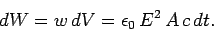 |
(334) |
It follows, from the definition of  , that the power per unit area carried by
the wave is given by
, that the power per unit area carried by
the wave is given by
 |
(335) |
so that
 |
(336) |
Since half the energy in an electromagnetic wave is carried by the
electric field, and the other half is carried by the magnetic field, it
is conventional to convert the above expression into a form involving both
the electric and magnetic field strengths. Since, 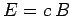 , we have
, we have
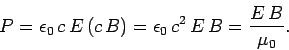 |
(337) |
Thus,
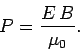 |
(338) |
Equation (338) specifies the power per unit area transported by an electromagnetic
wave at any given instant of time. The peak power is given by
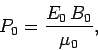 |
(339) |
where 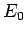 and
and 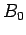 are the peak amplitudes of the oscillatory
electric and
magnetic fields, respectively. It is easily demonstrated that
the average power per unit area transported by an electromagnetic wave
is half the peak power, so that
are the peak amplitudes of the oscillatory
electric and
magnetic fields, respectively. It is easily demonstrated that
the average power per unit area transported by an electromagnetic wave
is half the peak power, so that
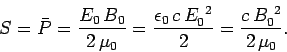 |
(340) |
The quantity 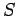 is conventionally termed the intensity of the wave.
is conventionally termed the intensity of the wave.



Next: Worked Examples
Up: Electromagnetic Waves
Previous: Effect of Dielectric Materials
Richard Fitzpatrick
2007-07-14
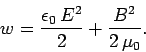
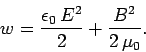
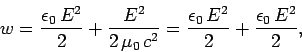
![]() be the
power per unit area carried by an electromagnetic wave:
i.e.,
be the
power per unit area carried by an electromagnetic wave:
i.e., ![]() is the energy transported per unit time
across a unit cross-sectional area perpendicular to the
direction in which the wave is traveling. Consider a
plane electromagnetic
wave propagating along the
is the energy transported per unit time
across a unit cross-sectional area perpendicular to the
direction in which the wave is traveling. Consider a
plane electromagnetic
wave propagating along the ![]() -axis. The wave propagates
a distance
-axis. The wave propagates
a distance ![]() along the
along the ![]() -axis in a time interval
-axis in a time interval ![]() . If we
consider a cross-sectional area
. If we
consider a cross-sectional area ![]() at right-angles to the
at right-angles to the ![]() -axis, then in
a time
-axis, then in
a time ![]() the wave sweeps through a volume
the wave sweeps through a volume ![]() of
space, where
of
space, where
![]() . The
amount of energy filling this volume is
. The
amount of energy filling this volume is