Next: Worked Examples
Up: Inductance
Previous: Transformers
The principle use of transformers is in
the transmission and distribution of commercially generated electricity.
However, a second, very important use of transformers is as impedance matching
devices. Recall, from Sect. 7.9, that for maximum
power delivery from a source
to a load, the load must have the same resistance as the internal resistance
of the source. This can be accomplished by using a transformer to match the two
resistances. Suppose that the power source is connected to the primary
circuit, and the load to the secondary.
If the resistance of the load is 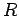 , then
, then
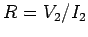 . However, from the transformer equation, (299), we have
. However, from the transformer equation, (299), we have
 |
(301) |
and
 |
(302) |
Now the effective resistance 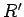 of the load in the primary circuit
is given by
of the load in the primary circuit
is given by
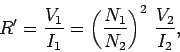 |
(303) |
which easily reduces to
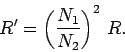 |
(304) |
Thus, by choosing the appropriate turns ratio, the effective load resistance
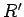 can be made equal to the internal resistance of the source, no matter what
value the
actual load resistance
can be made equal to the internal resistance of the source, no matter what
value the
actual load resistance 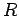 takes. This process is called impedance matching.
takes. This process is called impedance matching.



Next: Worked Examples
Up: Inductance
Previous: Transformers
Richard Fitzpatrick
2007-07-14