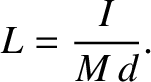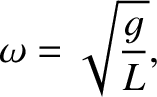Compound Pendulum
Consider an extended laminar object of mass  with a hole drilled though it. Suppose that the body is suspended
from a fixed horizontal peg, which passes through the hole, such that it is free to swing from side to side in a vertical plane,
as shown in Figure 1.9. This setup is known as a compound pendulum.
with a hole drilled though it. Suppose that the body is suspended
from a fixed horizontal peg, which passes through the hole, such that it is free to swing from side to side in a vertical plane,
as shown in Figure 1.9. This setup is known as a compound pendulum.
Figure 1.9:
A compound pendulum.
|
|
Let  be the pivot point, and let
be the pivot point, and let  be the body's center of mass, which is located a distance
be the body's center of mass, which is located a distance  from the
pivot. Let
from the
pivot. Let  be the angle subtended between the downward vertical (which passes through point
be the angle subtended between the downward vertical (which passes through point 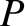 ) and the
line
) and the
line 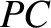 (which is assumed to be confined to a vertical plane). The equilibrium state of the compound pendulum corresponds to the case in which the center of
mass lies vertically below the pivot point; that is,
(which is assumed to be confined to a vertical plane). The equilibrium state of the compound pendulum corresponds to the case in which the center of
mass lies vertically below the pivot point; that is, 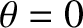 .
The angular equation of motion of the pendulum is
.
The angular equation of motion of the pendulum is
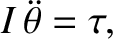 |
(1.55) |
where 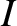 is the moment of inertia about the pivot, and
is the moment of inertia about the pivot, and 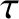 is the torque.
Using similar arguments to those employed for the case of the simple pendulum (recalling that
the weight of the pendulum acts at its center of mass), we can write
is the torque.
Using similar arguments to those employed for the case of the simple pendulum (recalling that
the weight of the pendulum acts at its center of mass), we can write
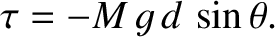 |
(1.56) |
The reaction,  , at the peg does not contribute to the torque, because its line of action passes
through the pivot.
Combining the previous two equations, we obtain the following angular equation of motion of the pendulum,
, at the peg does not contribute to the torque, because its line of action passes
through the pivot.
Combining the previous two equations, we obtain the following angular equation of motion of the pendulum,
 |
(1.57) |
Finally, adopting the small-angle approximation,
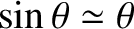 , we arrive at the
simple harmonic oscillator equation,
, we arrive at the
simple harmonic oscillator equation,
 |
(1.58) |
By analogy with our previous solutions of such equations, the angular frequency of small
amplitude oscillations of a compound pendulum is given by
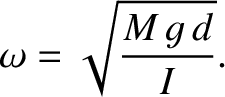 |
(1.59) |
It is helpful to define the so-called effective length of the pendulum,
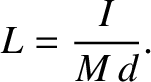 |
(1.60) |
Equation (1.59) reduces to
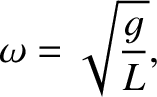 |
(1.61) |
which is identical in form to the corresponding expression for a simple pendulum. (See Section 1.5.) We conclude that a
compound pendulum behaves like a simple pendulum whose length is equal to the effective length.
 with a hole drilled though it. Suppose that the body is suspended
from a fixed horizontal peg, which passes through the hole, such that it is free to swing from side to side in a vertical plane,
as shown in Figure 1.9. This setup is known as a compound pendulum.
with a hole drilled though it. Suppose that the body is suspended
from a fixed horizontal peg, which passes through the hole, such that it is free to swing from side to side in a vertical plane,
as shown in Figure 1.9. This setup is known as a compound pendulum.
 be the pivot point, and let
be the pivot point, and let  be the body's center of mass, which is located a distance
be the body's center of mass, which is located a distance  from the
pivot. Let
from the
pivot. Let 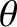 be the angle subtended between the downward vertical (which passes through point
be the angle subtended between the downward vertical (which passes through point 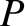 ) and the
line
) and the
line 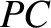 (which is assumed to be confined to a vertical plane). The equilibrium state of the compound pendulum corresponds to the case in which the center of
mass lies vertically below the pivot point; that is,
(which is assumed to be confined to a vertical plane). The equilibrium state of the compound pendulum corresponds to the case in which the center of
mass lies vertically below the pivot point; that is, 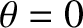 .
The angular equation of motion of the pendulum is
.
The angular equation of motion of the pendulum is
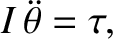
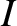 is the moment of inertia about the pivot, and
is the moment of inertia about the pivot, and 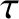 is the torque.
Using similar arguments to those employed for the case of the simple pendulum (recalling that
the weight of the pendulum acts at its center of mass), we can write
is the torque.
Using similar arguments to those employed for the case of the simple pendulum (recalling that
the weight of the pendulum acts at its center of mass), we can write
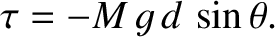
 , at the peg does not contribute to the torque, because its line of action passes
through the pivot.
Combining the previous two equations, we obtain the following angular equation of motion of the pendulum,
, at the peg does not contribute to the torque, because its line of action passes
through the pivot.
Combining the previous two equations, we obtain the following angular equation of motion of the pendulum,

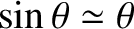 , we arrive at the
simple harmonic oscillator equation,
, we arrive at the
simple harmonic oscillator equation,