Driven LCR Circuit
Figure 2.6:
A driven LCR circuit.
|
|
Consider an LCR circuit consisting of an inductor, 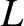 , a capacitor,
, a capacitor,  , and a resistor,
, and a resistor, 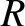 , connected
in series with an oscillating emf of voltage
, connected
in series with an oscillating emf of voltage 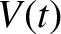 . See Figure 2.6. Let
. See Figure 2.6. Let
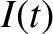 be the instantaneous current flowing around the circuit.
According to
Kirchhoff's second circuital law, the sum of the potential drops across the
various components of a closed circuit loop is equal to zero. Thus, because the
potential drop across an emf is minus the associated voltage (Fitzpatrick 2008),
we obtain [cf., Equation (2.32)]
be the instantaneous current flowing around the circuit.
According to
Kirchhoff's second circuital law, the sum of the potential drops across the
various components of a closed circuit loop is equal to zero. Thus, because the
potential drop across an emf is minus the associated voltage (Fitzpatrick 2008),
we obtain [cf., Equation (2.32)]
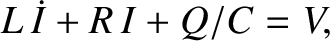 |
(2.63) |
where 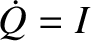 . Suppose that the emf is such that its voltage oscillates
sinusoidally at the angular frequency
. Suppose that the emf is such that its voltage oscillates
sinusoidally at the angular frequency 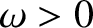 , with the peak value
, with the peak value
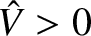 , so that
, so that
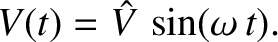 |
(2.64) |
Dividing Equation (2.63) by  , and differentiating with respect to time,
we obtain [cf., Equation (2.33)]
, and differentiating with respect to time,
we obtain [cf., Equation (2.33)]
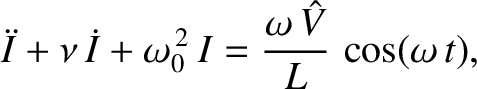 |
(2.65) |
where
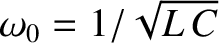 and
and 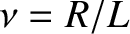 . Comparison with Equation (2.43) reveals that this is a driven damped harmonic oscillator equation.
It follows, by analogy with the analysis contained in the previous section, that
the current driven in the circuit by the oscillating emf is of the form
. Comparison with Equation (2.43) reveals that this is a driven damped harmonic oscillator equation.
It follows, by analogy with the analysis contained in the previous section, that
the current driven in the circuit by the oscillating emf is of the form
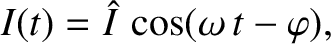 |
(2.66) |
where
In the immediate vicinity of the resonance (i.e.,
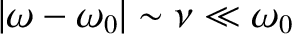 ), these expression simplify to
The circuit's mean power absorption from the emf is written
), these expression simplify to
The circuit's mean power absorption from the emf is written
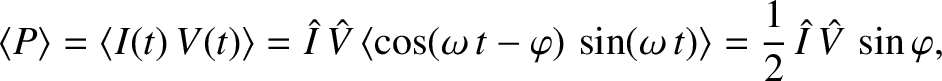 |
(2.71) |
so that
![$\displaystyle \langle P\rangle \simeq \frac{1}{2}\,\frac{\skew{3}\hat{V}^{\,2}}{R}\left[\frac{\nu^{\,2}}{4\,(\omega_0-\omega)^{\,2}+\nu^{\,2}}\right]$](img586.png) |
(2.72) |
close to the resonance.
It follows that the peak power absorption,
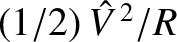 , takes place when the
emf oscillates at the resonant frequency,
, takes place when the
emf oscillates at the resonant frequency, 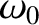 . Moreover, the power absorption falls
to half of this peak value at the edges of the resonant peak; that is,
. Moreover, the power absorption falls
to half of this peak value at the edges of the resonant peak; that is,
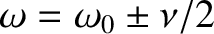 .
.
LCR circuits can be used as analog radio tuners. In this application,
the emf represents the analog signal picked up by a radio antenna. According to the
previous analysis, the circuit only has a strong response (i.e., it only absorbs significant energy) when
the signal oscillates in the angular frequency range
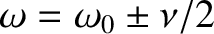 , which corresponds
to
, which corresponds
to
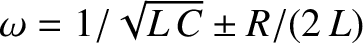 . Thus, if the values of
. Thus, if the values of 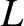 ,
,  , and
, and 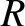 are
properly chosen then the circuit can be made to strongly absorb the signal from a
particular radio station, which has a given carrier frequency and bandwidth (see Section 8.5), while essentially ignoring the signals from other stations
with different carrier frequencies. In practice, the values of
are
properly chosen then the circuit can be made to strongly absorb the signal from a
particular radio station, which has a given carrier frequency and bandwidth (see Section 8.5), while essentially ignoring the signals from other stations
with different carrier frequencies. In practice, the values of 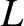 and
and 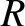 are fixed,
while the value of
are fixed,
while the value of  is varied (by turning a knob that adjusts the degree of overlap
between two sets of parallel semicircular conducting plates) until the signal from the desired radio
station is found.
is varied (by turning a knob that adjusts the degree of overlap
between two sets of parallel semicircular conducting plates) until the signal from the desired radio
station is found.
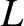 , a capacitor,
, a capacitor,  , and a resistor,
, and a resistor, 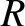 , connected
in series with an oscillating emf of voltage
, connected
in series with an oscillating emf of voltage 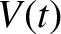 . See Figure 2.6. Let
. See Figure 2.6. Let
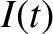 be the instantaneous current flowing around the circuit.
According to
Kirchhoff's second circuital law, the sum of the potential drops across the
various components of a closed circuit loop is equal to zero. Thus, because the
potential drop across an emf is minus the associated voltage (Fitzpatrick 2008),
we obtain [cf., Equation (2.32)]
be the instantaneous current flowing around the circuit.
According to
Kirchhoff's second circuital law, the sum of the potential drops across the
various components of a closed circuit loop is equal to zero. Thus, because the
potential drop across an emf is minus the associated voltage (Fitzpatrick 2008),
we obtain [cf., Equation (2.32)]
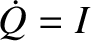 . Suppose that the emf is such that its voltage oscillates
sinusoidally at the angular frequency
. Suppose that the emf is such that its voltage oscillates
sinusoidally at the angular frequency 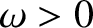 , with the peak value
, with the peak value
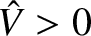 , so that
, so that
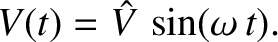
 , and differentiating with respect to time,
we obtain [cf., Equation (2.33)]
, and differentiating with respect to time,
we obtain [cf., Equation (2.33)]
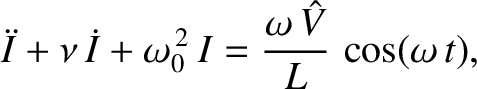
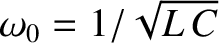 and
and 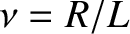 . Comparison with Equation (2.43) reveals that this is a driven damped harmonic oscillator equation.
It follows, by analogy with the analysis contained in the previous section, that
the current driven in the circuit by the oscillating emf is of the form
. Comparison with Equation (2.43) reveals that this is a driven damped harmonic oscillator equation.
It follows, by analogy with the analysis contained in the previous section, that
the current driven in the circuit by the oscillating emf is of the form
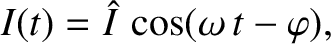
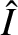
![$\displaystyle =\frac{\omega\,\skew{3}\hat{V}/L}{\left[(\omega_0^{\,2}-\omega^{\,2})^{\,2}+\nu^{\,2}\,\omega^{\,2}\right]^{1/2}},$](img582.png)
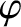
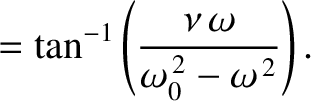
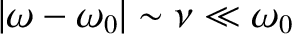 ), these expression simplify to
), these expression simplify to
![$\displaystyle \simeq \frac{\skew{3}\hat{V}}{R}\,\frac{\nu}{\left[4\,(\omega_0-\omega)^{\,2}+\nu^{\,2}\right]^{1/2}},$](img583.png)
![$\displaystyle \simeq \frac{\nu}{\left[4\,(\omega-\omega_0)^{\,2}+\nu^{\,2}\right]^{1/2}}.$](img584.png)
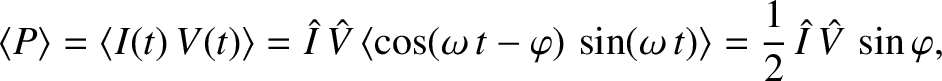
![$\displaystyle \langle P\rangle \simeq \frac{1}{2}\,\frac{\skew{3}\hat{V}^{\,2}}{R}\left[\frac{\nu^{\,2}}{4\,(\omega_0-\omega)^{\,2}+\nu^{\,2}}\right]$](img586.png)
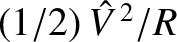 , takes place when the
emf oscillates at the resonant frequency,
, takes place when the
emf oscillates at the resonant frequency, 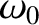 . Moreover, the power absorption falls
to half of this peak value at the edges of the resonant peak; that is,
. Moreover, the power absorption falls
to half of this peak value at the edges of the resonant peak; that is,
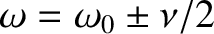 .
.
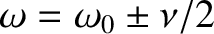 , which corresponds
to
, which corresponds
to
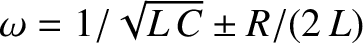 . Thus, if the values of
. Thus, if the values of  ,
,  , and
, and  are
properly chosen then the circuit can be made to strongly absorb the signal from a
particular radio station, which has a given carrier frequency and bandwidth (see Section 8.5), while essentially ignoring the signals from other stations
with different carrier frequencies. In practice, the values of
are
properly chosen then the circuit can be made to strongly absorb the signal from a
particular radio station, which has a given carrier frequency and bandwidth (see Section 8.5), while essentially ignoring the signals from other stations
with different carrier frequencies. In practice, the values of 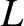 and
and 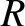 are fixed,
while the value of
are fixed,
while the value of  is varied (by turning a knob that adjusts the degree of overlap
between two sets of parallel semicircular conducting plates) until the signal from the desired radio
station is found.
is varied (by turning a knob that adjusts the degree of overlap
between two sets of parallel semicircular conducting plates) until the signal from the desired radio
station is found.