Pulse Propagation
Consider a one-dimensional wave pulse,
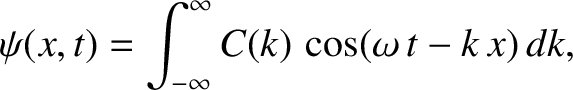 |
(9.1) |
made up of a linear superposition of cosine waves, with a range of different wavenumbers, all
traveling in the positive  -direction. The angular frequency,
-direction. The angular frequency, 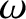 ,
of each of these waves is related to its wavenumber,
,
of each of these waves is related to its wavenumber,  , via the so-called
dispersion relation, which can be written schematically as
, via the so-called
dispersion relation, which can be written schematically as
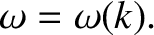 |
(9.2) |
In general, this relation is derivable from the wave disturbance's equation of motion.
Up to now, we have only considered sinusoidal waves that have linear dispersion
relations of the form
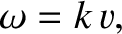 |
(9.3) |
where 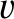 is a constant. The previous expression immediately implies that such waves have the same phase velocity,
is a constant. The previous expression immediately implies that such waves have the same phase velocity,
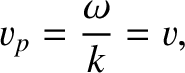 |
(9.4) |
irrespective of their frequencies.
Substituting Equation (9.3) into Equation (9.1),
we obtain
![$\displaystyle \psi(x,t)=\int_{-\infty}^\infty C(k)\,\cos[k\,(v\,t-x)]\,dk,$](img2546.png) |
(9.5) |
which is the equation of a wave pulse that propagates in the positive
 -direction, at the fixed speed
-direction, at the fixed speed 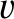 , without changing shape. (See Chapter 8.) The previous analysis
seems to suggest that arbitrarily-shaped wave pulses generally propagate at the same speed as sinusoidal
waves, and do so without dispersing or, otherwise, changing shape. In fact,
these statements are only true of pulses made up of superpositions of sinusoidal waves with linear dispersion
relations. There are, however, many types of sinusoidal wave whose dispersion relations
are nonlinear. For instance, the dispersion relation of sinusoidal
electromagnetic waves propagating through an unmagnetized plasma is (see Section 9.3)
, without changing shape. (See Chapter 8.) The previous analysis
seems to suggest that arbitrarily-shaped wave pulses generally propagate at the same speed as sinusoidal
waves, and do so without dispersing or, otherwise, changing shape. In fact,
these statements are only true of pulses made up of superpositions of sinusoidal waves with linear dispersion
relations. There are, however, many types of sinusoidal wave whose dispersion relations
are nonlinear. For instance, the dispersion relation of sinusoidal
electromagnetic waves propagating through an unmagnetized plasma is (see Section 9.3)
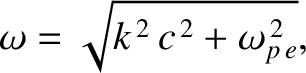 |
(9.6) |
where 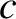 is the speed of light in vacuum, and
is the speed of light in vacuum, and
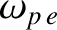 is a
constant, known as the (electron) plasma frequency, that depends on the properties of
the plasma. [See Equation (9.28).] Moreover,
the dispersion relation of sinusoidal surface waves in deep
water is
is a
constant, known as the (electron) plasma frequency, that depends on the properties of
the plasma. [See Equation (9.28).] Moreover,
the dispersion relation of sinusoidal surface waves in deep
water is
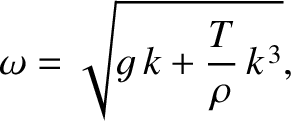 |
(9.7) |
where 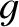 is the acceleration due to gravity,
is the acceleration due to gravity, 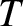 the surface tension of water, and
the surface tension of water, and 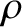 the mass density. Sinusoidal waves that satisfy nonlinear dispersion relations, such as (9.6) or (9.7), are known
as dispersive waves, as opposed to waves that satisfy linear
dispersion relations, such as (9.3), which are called non-dispersive waves. As we saw previously, a wave pulse made up of a linear superposition of non-dispersive sinusoidal waves,
all traveling in the same direction, propagates at the common phase velocity
of these waves, without changing shape. How does a wave pulse
made up of a linear superposition of dispersive sinusoidal waves evolve in time?
the mass density. Sinusoidal waves that satisfy nonlinear dispersion relations, such as (9.6) or (9.7), are known
as dispersive waves, as opposed to waves that satisfy linear
dispersion relations, such as (9.3), which are called non-dispersive waves. As we saw previously, a wave pulse made up of a linear superposition of non-dispersive sinusoidal waves,
all traveling in the same direction, propagates at the common phase velocity
of these waves, without changing shape. How does a wave pulse
made up of a linear superposition of dispersive sinusoidal waves evolve in time?
Suppose that
![$\displaystyle C(k) = \frac{1}{\sqrt{2\pi\,\sigma_k^{\,2}}}\,\exp\left[-\frac{(k-k_0)^{\,2}}{2\,\sigma_k^{\,2}}\right].$](img2550.png) |
(9.8) |
In other words, the function 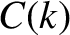 in Equation (9.1) is a Gaussian, of characteristic width
in Equation (9.1) is a Gaussian, of characteristic width 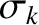 , centered on wavenumber
, centered on wavenumber 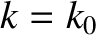 . It follows, from the properties of the
Gaussian function, that
. It follows, from the properties of the
Gaussian function, that 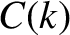 is negligible for
is negligible for
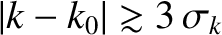 .
Thus, the only significant contributions to the wave
integral
.
Thus, the only significant contributions to the wave
integral
![$\displaystyle \psi(x,t) = \int_{-\infty}^\infty\frac{1}{\sqrt{2\pi\,\sigma_k^{\...
...xp\left[-\frac{(k-k_0)^{\,2}}{2\,\sigma_k^{\,2}}\right]\cos(\omega\,t-k\,x)\,dk$](img2554.png) |
(9.9) |
come from a small region of  -space centered on
-space centered on 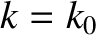 . Let us
Taylor expand the dispersion relation,
. Let us
Taylor expand the dispersion relation,
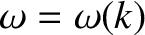 , about
, about 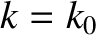 .
Neglecting second-order terms in the expansion, we obtain
.
Neglecting second-order terms in the expansion, we obtain
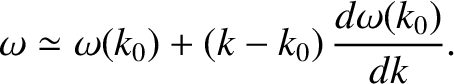 |
(9.10) |
It follows that
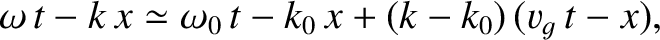 |
(9.11) |
where
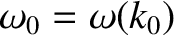 , and
, and
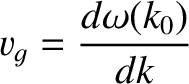 |
(9.12) |
is a constant with the dimensions of velocity.
If 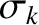 is sufficiently small then the neglect of second-order terms in the expansion (9.11) is a good approximation, and Equation (9.9) becomes
where use has been made of a standard trigonometric identity. (See Appendix B.)
The integral involving
is sufficiently small then the neglect of second-order terms in the expansion (9.11) is a good approximation, and Equation (9.9) becomes
where use has been made of a standard trigonometric identity. (See Appendix B.)
The integral involving
![$\sin[(k-k_0)\,(v_g\,t-x)]$](img2562.png) is zero, by symmetry. Moreover,
an examination of Equations (8.15)–(8.18) reveals that
is zero, by symmetry. Moreover,
an examination of Equations (8.15)–(8.18) reveals that
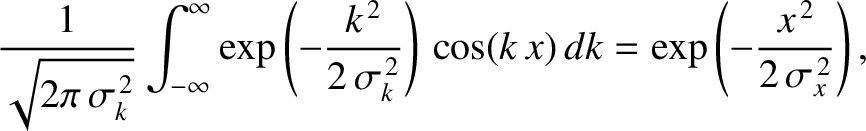 |
(9.14) |
where
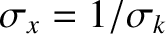 . Hence, by analogy with this expression, Equation (9.13) reduces to
. Hence, by analogy with this expression, Equation (9.13) reduces to
![$\displaystyle \psi(x,t)\simeq \exp\left[-\frac{(v_g\,t-x)^{\,2}}{2\,\sigma_x^{\,2}}\right]\,\cos(\omega_0\,t-k_0\,x).$](img2565.png) |
(9.15) |
This is the equation of a wave pulse, of wavenumber 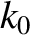 , and angular frequency
, and angular frequency 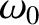 ,
with a Gaussian envelope, of characteristic width
,
with a Gaussian envelope, of characteristic width 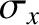 , whose peak (which is located by setting the argument of the exponential to zero) has the
equation of motion
, whose peak (which is located by setting the argument of the exponential to zero) has the
equation of motion
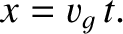 |
(9.16) |
In other words, the pulse peak—and, hence, the pulse itself—propagates at
the velocity 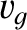 , which is known as the group velocity. In the case of non-dispersive waves, the group
velocity is the same as the phase velocity (because, if
, which is known as the group velocity. In the case of non-dispersive waves, the group
velocity is the same as the phase velocity (because, if
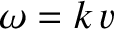 then
then
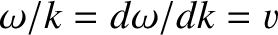 ). However, for the case of dispersive waves, the two velocities are, in general,
different.
). However, for the case of dispersive waves, the two velocities are, in general,
different.
Equation (9.15) indicates that, as the wave pulse propagates, its envelope
remains the same shape. Actually, this result is misleading, and is only obtained because
of the neglect of second-order terms in the expansion (9.11). If we keep more terms in this expansion then we can show that the wave pulse
does actually change shape as it propagates. However, this demonstration is most readily effected by means of the
following simple argument. The pulse extends in Fourier space from
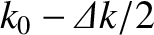 to
to
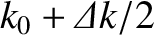 , where
, where
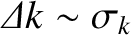 . Thus, part of the pulse
propagates at the velocity
. Thus, part of the pulse
propagates at the velocity
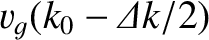 , and part at the
velocity
, and part at the
velocity
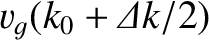 . Consequently, the pulse spreads out as it propagates, because some parts of it move faster than others.
Roughly speaking, the spatial extent of the pulse in real space grows as
. Consequently, the pulse spreads out as it propagates, because some parts of it move faster than others.
Roughly speaking, the spatial extent of the pulse in real space grows as
![$\displaystyle {\mit\Delta} x\sim ({\mit\Delta} x)_0+ \left[v_g(k_0+{\mit\Delta}...
...} k/2)\right] t\sim
({\mit\Delta} x)_0+\frac{dv_g(k_0)}{dk}\,{\mit\Delta} k\,t,$](img2575.png) |
(9.17) |
where
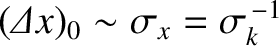 is the extent of the pulse at
is the extent of the pulse at  .
Hence, from Equation (9.12),
.
Hence, from Equation (9.12),
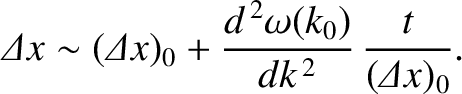 |
(9.18) |
We, thus, conclude that the spatial extent of the pulse grows linearly in time, at a rate
proportional to the second derivative of the dispersion relation with respect to  (evaluated at the pulse's central wavenumber). This effect is
known as pulse dispersion. Incidentally, there is no pulse dispersion in a non-dispersive
medium, because, by definition,
(evaluated at the pulse's central wavenumber). This effect is
known as pulse dispersion. Incidentally, there is no pulse dispersion in a non-dispersive
medium, because, by definition,
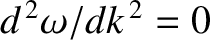 in such a medium.
In summary, a wave pulse made up of a linear superposition
of dispersive sinusoidal waves, with a range of different wavenumbers, propagates at the group velocity, and also gradually disperses as time progresses.
in such a medium.
In summary, a wave pulse made up of a linear superposition
of dispersive sinusoidal waves, with a range of different wavenumbers, propagates at the group velocity, and also gradually disperses as time progresses.
 -direction. The angular frequency,
-direction. The angular frequency, 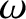 ,
of each of these waves is related to its wavenumber,
,
of each of these waves is related to its wavenumber,  , via the so-called
dispersion relation, which can be written schematically as
, via the so-called
dispersion relation, which can be written schematically as
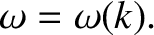
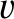 is a constant. The previous expression immediately implies that such waves have the same phase velocity,
is a constant. The previous expression immediately implies that such waves have the same phase velocity,
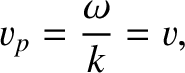
![$\displaystyle \psi(x,t)=\int_{-\infty}^\infty C(k)\,\cos[k\,(v\,t-x)]\,dk,$](img2546.png)
 -direction, at the fixed speed
-direction, at the fixed speed 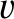 , without changing shape. (See Chapter 8.) The previous analysis
seems to suggest that arbitrarily-shaped wave pulses generally propagate at the same speed as sinusoidal
waves, and do so without dispersing or, otherwise, changing shape. In fact,
these statements are only true of pulses made up of superpositions of sinusoidal waves with linear dispersion
relations. There are, however, many types of sinusoidal wave whose dispersion relations
are nonlinear. For instance, the dispersion relation of sinusoidal
electromagnetic waves propagating through an unmagnetized plasma is (see Section 9.3)
where
, without changing shape. (See Chapter 8.) The previous analysis
seems to suggest that arbitrarily-shaped wave pulses generally propagate at the same speed as sinusoidal
waves, and do so without dispersing or, otherwise, changing shape. In fact,
these statements are only true of pulses made up of superpositions of sinusoidal waves with linear dispersion
relations. There are, however, many types of sinusoidal wave whose dispersion relations
are nonlinear. For instance, the dispersion relation of sinusoidal
electromagnetic waves propagating through an unmagnetized plasma is (see Section 9.3)
where 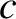 is the speed of light in vacuum, and
is the speed of light in vacuum, and
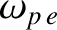 is a
constant, known as the (electron) plasma frequency, that depends on the properties of
the plasma. [See Equation (9.28).] Moreover,
the dispersion relation of sinusoidal surface waves in deep
water is
where
is a
constant, known as the (electron) plasma frequency, that depends on the properties of
the plasma. [See Equation (9.28).] Moreover,
the dispersion relation of sinusoidal surface waves in deep
water is
where 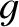 is the acceleration due to gravity,
is the acceleration due to gravity, 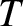 the surface tension of water, and
the surface tension of water, and 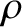 the mass density. Sinusoidal waves that satisfy nonlinear dispersion relations, such as (9.6) or (9.7), are known
as dispersive waves, as opposed to waves that satisfy linear
dispersion relations, such as (9.3), which are called non-dispersive waves. As we saw previously, a wave pulse made up of a linear superposition of non-dispersive sinusoidal waves,
all traveling in the same direction, propagates at the common phase velocity
of these waves, without changing shape. How does a wave pulse
made up of a linear superposition of dispersive sinusoidal waves evolve in time?
the mass density. Sinusoidal waves that satisfy nonlinear dispersion relations, such as (9.6) or (9.7), are known
as dispersive waves, as opposed to waves that satisfy linear
dispersion relations, such as (9.3), which are called non-dispersive waves. As we saw previously, a wave pulse made up of a linear superposition of non-dispersive sinusoidal waves,
all traveling in the same direction, propagates at the common phase velocity
of these waves, without changing shape. How does a wave pulse
made up of a linear superposition of dispersive sinusoidal waves evolve in time?
![$\displaystyle C(k) = \frac{1}{\sqrt{2\pi\,\sigma_k^{\,2}}}\,\exp\left[-\frac{(k-k_0)^{\,2}}{2\,\sigma_k^{\,2}}\right].$](img2550.png)
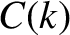 in Equation (9.1) is a Gaussian, of characteristic width
in Equation (9.1) is a Gaussian, of characteristic width 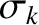 , centered on wavenumber
, centered on wavenumber 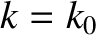 . It follows, from the properties of the
Gaussian function, that
. It follows, from the properties of the
Gaussian function, that 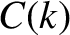 is negligible for
is negligible for
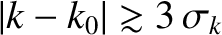 .
Thus, the only significant contributions to the wave
integral
come from a small region of
.
Thus, the only significant contributions to the wave
integral
come from a small region of  -space centered on
-space centered on 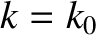 . Let us
Taylor expand the dispersion relation,
. Let us
Taylor expand the dispersion relation,
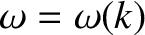 , about
, about 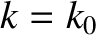 .
Neglecting second-order terms in the expansion, we obtain
It follows that
where
.
Neglecting second-order terms in the expansion, we obtain
It follows that
where
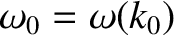 , and
is a constant with the dimensions of velocity.
If
, and
is a constant with the dimensions of velocity.
If 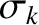 is sufficiently small then the neglect of second-order terms in the expansion (9.11) is a good approximation, and Equation (9.9) becomes
where use has been made of a standard trigonometric identity. (See Appendix B.)
The integral involving
is sufficiently small then the neglect of second-order terms in the expansion (9.11) is a good approximation, and Equation (9.9) becomes
where use has been made of a standard trigonometric identity. (See Appendix B.)
The integral involving
![$\sin[(k-k_0)\,(v_g\,t-x)]$](img2562.png) is zero, by symmetry. Moreover,
an examination of Equations (8.15)–(8.18) reveals that
is zero, by symmetry. Moreover,
an examination of Equations (8.15)–(8.18) reveals that
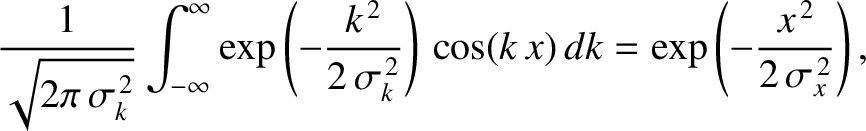
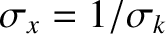 . Hence, by analogy with this expression, Equation (9.13) reduces to
This is the equation of a wave pulse, of wavenumber
. Hence, by analogy with this expression, Equation (9.13) reduces to
This is the equation of a wave pulse, of wavenumber 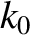 , and angular frequency
, and angular frequency 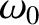 ,
with a Gaussian envelope, of characteristic width
,
with a Gaussian envelope, of characteristic width 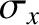 , whose peak (which is located by setting the argument of the exponential to zero) has the
equation of motion
, whose peak (which is located by setting the argument of the exponential to zero) has the
equation of motion
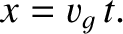
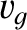 , which is known as the group velocity. In the case of non-dispersive waves, the group
velocity is the same as the phase velocity (because, if
, which is known as the group velocity. In the case of non-dispersive waves, the group
velocity is the same as the phase velocity (because, if
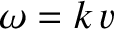 then
then
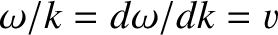 ). However, for the case of dispersive waves, the two velocities are, in general,
different.
). However, for the case of dispersive waves, the two velocities are, in general,
different.
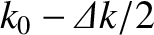 to
to
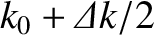 , where
, where
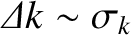 . Thus, part of the pulse
propagates at the velocity
. Thus, part of the pulse
propagates at the velocity
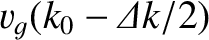 , and part at the
velocity
, and part at the
velocity
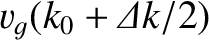 . Consequently, the pulse spreads out as it propagates, because some parts of it move faster than others.
Roughly speaking, the spatial extent of the pulse in real space grows as
. Consequently, the pulse spreads out as it propagates, because some parts of it move faster than others.
Roughly speaking, the spatial extent of the pulse in real space grows as
![$\displaystyle {\mit\Delta} x\sim ({\mit\Delta} x)_0+ \left[v_g(k_0+{\mit\Delta}...
...} k/2)\right] t\sim
({\mit\Delta} x)_0+\frac{dv_g(k_0)}{dk}\,{\mit\Delta} k\,t,$](img2575.png)
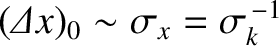 is the extent of the pulse at
is the extent of the pulse at 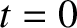 .
Hence, from Equation (9.12),
.
Hence, from Equation (9.12),
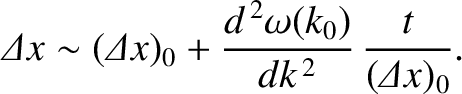
 (evaluated at the pulse's central wavenumber). This effect is
known as pulse dispersion. Incidentally, there is no pulse dispersion in a non-dispersive
medium, because, by definition,
(evaluated at the pulse's central wavenumber). This effect is
known as pulse dispersion. Incidentally, there is no pulse dispersion in a non-dispersive
medium, because, by definition,
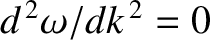 in such a medium.
In summary, a wave pulse made up of a linear superposition
of dispersive sinusoidal waves, with a range of different wavenumbers, propagates at the group velocity, and also gradually disperses as time progresses.
in such a medium.
In summary, a wave pulse made up of a linear superposition
of dispersive sinusoidal waves, with a range of different wavenumbers, propagates at the group velocity, and also gradually disperses as time progresses.