Next: Spherical Waves Up: Multi-Dimensional Waves Previous: Three-Dimensional Wave Equation Contents
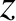 -axis) wavefunction
-axis) wavefunction
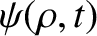 , where
, where
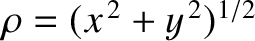 is a standard radial
cylindrical coordinate (Fitzpatrick 2008). Assuming that this function satisfies the three-dimensional wave equation, (7.9), which
can be rewritten (see Exercise 2)
it can be shown (see Exercise 2) that a sinusoidal cylindrical wave of phase angle
is a standard radial
cylindrical coordinate (Fitzpatrick 2008). Assuming that this function satisfies the three-dimensional wave equation, (7.9), which
can be rewritten (see Exercise 2)
it can be shown (see Exercise 2) that a sinusoidal cylindrical wave of phase angle  , wavenumber
, wavenumber  , and angular frequency
, and angular frequency
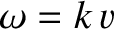 , has the
approximate wavefunction
in the limit
, has the
approximate wavefunction
in the limit
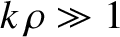 . Here,
. Here,
 is the amplitude of the wave.
The associated wavefronts (i.e., the surfaces of constant phase) are a set of concentric cylinders that
propagate radially outward, from their common axis (
is the amplitude of the wave.
The associated wavefronts (i.e., the surfaces of constant phase) are a set of concentric cylinders that
propagate radially outward, from their common axis (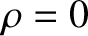 ), at the phase velocity
), at the phase velocity
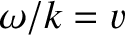 . See Figure 7.3. The wave amplitude attenuates as
. See Figure 7.3. The wave amplitude attenuates as
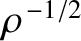 .
Such behavior can be understood as a consequence of energy conservation, according to which the power flowing across the various
.
Such behavior can be understood as a consequence of energy conservation, according to which the power flowing across the various
 surfaces must be
constant. (The areas of such surfaces scale as
surfaces must be
constant. (The areas of such surfaces scale as
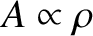 .
Moreover, the power flowing across them is proportional to
.
Moreover, the power flowing across them is proportional to
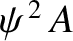 , because the energy flux associated with
a wave is generally proportional to
, because the energy flux associated with
a wave is generally proportional to
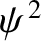 , and is directed normal to the wavefronts.)
The cylindrical wave specified in expression (7.11) is such as would be generated by
a uniform line source located at
, and is directed normal to the wavefronts.)
The cylindrical wave specified in expression (7.11) is such as would be generated by
a uniform line source located at 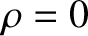 . See Figure 7.3.
. See Figure 7.3.