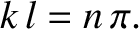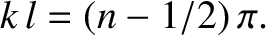Standing Waves in Finite Continuous Medium
We saw earlier, in Sections 4.3 and 5.2,
that a small-amplitude transverse wave on a uniform string, and a small-amplitude longitudinal
wave on a thin elastic rod, are both governed by the
wave equation, which (in one dimension) takes the general form
 |
(6.1) |
where 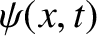 represents the wave disturbance, and
represents the wave disturbance, and 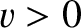 is a constant, with the dimensions
of velocity, that is a property of the particular medium that supports the wave. Up to now, we have only considered media of finite length. That is, media that extend from (say)
is a constant, with the dimensions
of velocity, that is a property of the particular medium that supports the wave. Up to now, we have only considered media of finite length. That is, media that extend from (say)
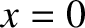 to
to 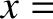
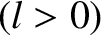 . Generally speaking, we have encountered two distinct types of physical
constraint that hold at the boundaries of such media. First, if a given boundary is
fixed then the wave disturbance is constrained to be zero there. For instance, if the left boundary is fixed then
. Generally speaking, we have encountered two distinct types of physical
constraint that hold at the boundaries of such media. First, if a given boundary is
fixed then the wave disturbance is constrained to be zero there. For instance, if the left boundary is fixed then
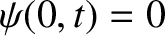 . Second, if a given boundary is free then the spatial derivative
of the disturbance (which usually corresponds to some sort of force) is constrained to be
zero there. For instance, if the right boundary is free then
. Second, if a given boundary is free then the spatial derivative
of the disturbance (which usually corresponds to some sort of force) is constrained to be
zero there. For instance, if the right boundary is free then
 . It follows that a fixed boundary corresponds to a node; that is,
a point where the amplitude of the wave disturbance is always zero. On the other hand, a
free boundary corresponds to an anti-node; that is, a point where the
amplitude of the wave disturbance is always locally maximal. Consequently, the
nodes and the anti-nodes of a wave, of definite wavelength, supported in a medium of finite length that has stationary boundaries (which can be either fixed or free) are constrained to be stationary. The only simple solution of the wave equation,
(6.1), that has stationary nodes and anti-nodes is a standing wave of the general form
. It follows that a fixed boundary corresponds to a node; that is,
a point where the amplitude of the wave disturbance is always zero. On the other hand, a
free boundary corresponds to an anti-node; that is, a point where the
amplitude of the wave disturbance is always locally maximal. Consequently, the
nodes and the anti-nodes of a wave, of definite wavelength, supported in a medium of finite length that has stationary boundaries (which can be either fixed or free) are constrained to be stationary. The only simple solution of the wave equation,
(6.1), that has stationary nodes and anti-nodes is a standing wave of the general form
![$\displaystyle \psi(x,t) =[A\,\cos(k\,x)+B\,\sin(k\,x)]\,\cos(\omega\,t-\phi).$](img1332.png) |
(6.2) |
The associated nodes are located at the values of  that satisfy
that satisfy
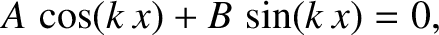 |
(6.3) |
which implies that they are stationary, and also evenly spaced a distance 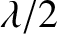 apart, where
apart, where
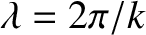 is the wavelength. Moreover, the anti-nodes
are situated halfway between the nodes. For example, suppose that both boundaries
of the medium
are fixed. It follows that the points
is the wavelength. Moreover, the anti-nodes
are situated halfway between the nodes. For example, suppose that both boundaries
of the medium
are fixed. It follows that the points 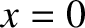 and
and 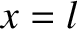 must each correspond to a node. This is
only possible if the length of the medium,
must each correspond to a node. This is
only possible if the length of the medium, 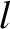 , is a half-integer number of wavelengths; that is,
, is a half-integer number of wavelengths; that is,
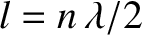 , where
, where  is a positive integer. We conclude that, in this case, the possible
wavenumbers of standing wave solutions to the wave equation are quantized such that
is a positive integer. We conclude that, in this case, the possible
wavenumbers of standing wave solutions to the wave equation are quantized such that
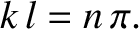 |
(6.4) |
Moreover, the same is true if both boundaries are free. Finally, if one boundary is free, and the
other fixed, then the quantization of wavenumbers takes the slightly different form
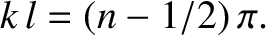 |
(6.5) |
Those standing wave solutions that satisfy the appropriate quantization criterion are known as the
normal modes of the system. (See Chapter 3.) Moreover, substitution of Equation (6.2)
into the wave equation, (6.1), yields the standing wave dispersion relation
 |
(6.6) |
The fact that normal mode wavenumbers are quantized immediately implies that the associated
oscillation frequencies are also quantized. Finally, because the
wave equation is linear, the most general solution that satisfies the
boundary conditions is a linear superposition of all of the normal modes. Such a
solution has the appropriate node or anti-node at each of the boundaries, but
does not necessarily have any stationary nodes or anti-nodes in the interior of the medium.
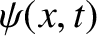 represents the wave disturbance, and
represents the wave disturbance, and 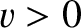 is a constant, with the dimensions
of velocity, that is a property of the particular medium that supports the wave. Up to now, we have only considered media of finite length. That is, media that extend from (say)
is a constant, with the dimensions
of velocity, that is a property of the particular medium that supports the wave. Up to now, we have only considered media of finite length. That is, media that extend from (say)
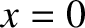 to
to 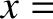
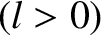 . Generally speaking, we have encountered two distinct types of physical
constraint that hold at the boundaries of such media. First, if a given boundary is
fixed then the wave disturbance is constrained to be zero there. For instance, if the left boundary is fixed then
. Generally speaking, we have encountered two distinct types of physical
constraint that hold at the boundaries of such media. First, if a given boundary is
fixed then the wave disturbance is constrained to be zero there. For instance, if the left boundary is fixed then
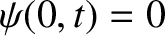 . Second, if a given boundary is free then the spatial derivative
of the disturbance (which usually corresponds to some sort of force) is constrained to be
zero there. For instance, if the right boundary is free then
. Second, if a given boundary is free then the spatial derivative
of the disturbance (which usually corresponds to some sort of force) is constrained to be
zero there. For instance, if the right boundary is free then
 . It follows that a fixed boundary corresponds to a node; that is,
a point where the amplitude of the wave disturbance is always zero. On the other hand, a
free boundary corresponds to an anti-node; that is, a point where the
amplitude of the wave disturbance is always locally maximal. Consequently, the
nodes and the anti-nodes of a wave, of definite wavelength, supported in a medium of finite length that has stationary boundaries (which can be either fixed or free) are constrained to be stationary. The only simple solution of the wave equation,
(6.1), that has stationary nodes and anti-nodes is a standing wave of the general form
The associated nodes are located at the values of
. It follows that a fixed boundary corresponds to a node; that is,
a point where the amplitude of the wave disturbance is always zero. On the other hand, a
free boundary corresponds to an anti-node; that is, a point where the
amplitude of the wave disturbance is always locally maximal. Consequently, the
nodes and the anti-nodes of a wave, of definite wavelength, supported in a medium of finite length that has stationary boundaries (which can be either fixed or free) are constrained to be stationary. The only simple solution of the wave equation,
(6.1), that has stationary nodes and anti-nodes is a standing wave of the general form
The associated nodes are located at the values of  that satisfy
that satisfy
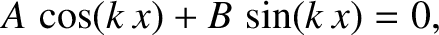
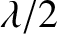 apart, where
apart, where
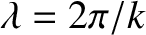 is the wavelength. Moreover, the anti-nodes
are situated halfway between the nodes. For example, suppose that both boundaries
of the medium
are fixed. It follows that the points
is the wavelength. Moreover, the anti-nodes
are situated halfway between the nodes. For example, suppose that both boundaries
of the medium
are fixed. It follows that the points 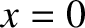 and
and 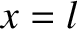 must each correspond to a node. This is
only possible if the length of the medium,
must each correspond to a node. This is
only possible if the length of the medium, 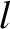 , is a half-integer number of wavelengths; that is,
, is a half-integer number of wavelengths; that is,
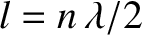 , where
, where  is a positive integer. We conclude that, in this case, the possible
wavenumbers of standing wave solutions to the wave equation are quantized such that
is a positive integer. We conclude that, in this case, the possible
wavenumbers of standing wave solutions to the wave equation are quantized such that