Quality Factor
The energy loss rate of a weakly damped (i.e.,
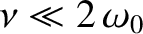 ) harmonic oscillator is conveniently
characterized in terms of a parameter,
) harmonic oscillator is conveniently
characterized in terms of a parameter,  , which is known as the
quality factor. (Note that the standard symbol for the quality factor is
, which is known as the
quality factor. (Note that the standard symbol for the quality factor is 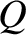 . We are only using
. We are only using
 here to avoid confusion with electrical charge.) This quantity is defined to be
here to avoid confusion with electrical charge.) This quantity is defined to be  times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and
times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and  is therefore
much larger than unity. Roughly speaking,
is therefore
much larger than unity. Roughly speaking,  is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value. (To be more exact,
is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value. (To be more exact,  is the number of oscillations that the
oscillator completes before its amplitude decays to about
is the number of oscillations that the
oscillator completes before its amplitude decays to about 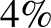 of its original value. See Exercise 6.) For instance, the quality factor for the
damped oscillation shown in Figure 2.1 is
of its original value. See Exercise 6.) For instance, the quality factor for the
damped oscillation shown in Figure 2.1 is 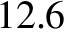 .
Let us find an expression for
.
Let us find an expression for  .
.
As we have seen, the motion of a weakly damped
harmonic oscillator is specified by [see Equation (2.12)]
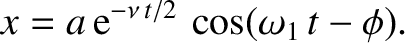 |
(2.23) |
It follows that
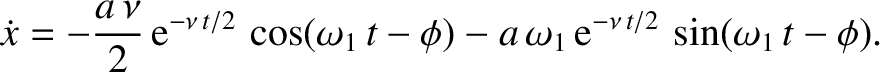 |
(2.24) |
Thus, making use of Equation (2.20), the energy lost during a single oscillation period is
In the weakly damped limit,
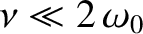 , the exponential factor is approximately
unity in the interval
, the exponential factor is approximately
unity in the interval
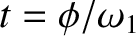 to
to
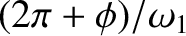 , so that
, so that
 |
(2.26) |
where
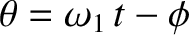 .
Thus,
.
Thus,
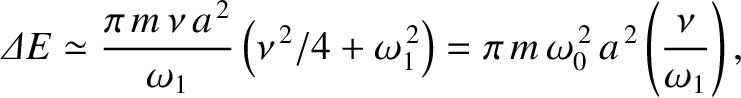 |
(2.27) |
because, as is readily demonstrated,
The energy stored in the oscillator
(at  ) is [cf., Equation (1.16)]
) is [cf., Equation (1.16)]
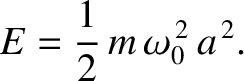 |
(2.30) |
Hence, we obtain
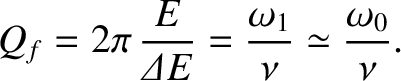 |
(2.31) |
 ) harmonic oscillator is conveniently
characterized in terms of a parameter,
) harmonic oscillator is conveniently
characterized in terms of a parameter,  , which is known as the
quality factor. (Note that the standard symbol for the quality factor is
, which is known as the
quality factor. (Note that the standard symbol for the quality factor is 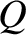 . We are only using
. We are only using
 here to avoid confusion with electrical charge.) This quantity is defined to be
here to avoid confusion with electrical charge.) This quantity is defined to be 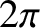 times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and
times the
energy stored in the oscillator, divided by the energy lost in a single
oscillation period. If the oscillator is weakly damped then
the energy lost per period is relatively small, and  is therefore
much larger than unity. Roughly speaking,
is therefore
much larger than unity. Roughly speaking,  is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value. (To be more exact,
is the number of oscillations
that the oscillator typically completes, after being set in motion, before its
amplitude decays to a negligible value. (To be more exact,  is the number of oscillations that the
oscillator completes before its amplitude decays to about
is the number of oscillations that the
oscillator completes before its amplitude decays to about 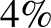 of its original value. See Exercise 6.) For instance, the quality factor for the
damped oscillation shown in Figure 2.1 is
of its original value. See Exercise 6.) For instance, the quality factor for the
damped oscillation shown in Figure 2.1 is 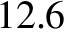 .
Let us find an expression for
.
Let us find an expression for  .
.
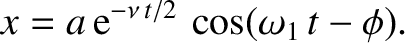
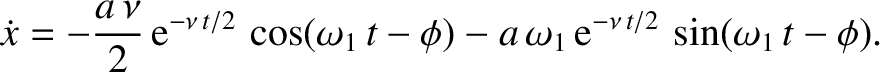
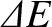
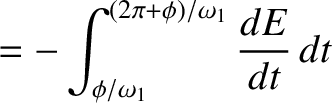
![$\displaystyle = m\,\nu\,a^{\,2}\int_{\phi/\omega_1}^{(2\pi+\phi)/\omega_1}{\rm ...
...{2}\,\cos(\omega_1\,t-\phi) + \omega_1\,\sin(\omega_1\,t-\phi)\right]^{\,2} dt.$](img481.png)
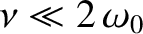 , the exponential factor is approximately
unity in the interval
, the exponential factor is approximately
unity in the interval
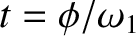 to
to
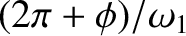 , so that
, so that

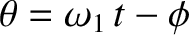 .
Thus,
.
Thus,
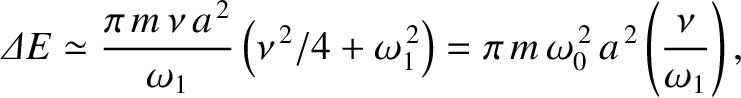
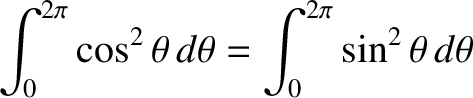


 ) is [cf., Equation (1.16)]
) is [cf., Equation (1.16)]