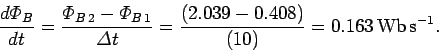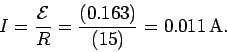Next: Worked Example 2: Lenz's
Up: Magnetic Induction
Previous: Worked Examples
Question: A plane circular loop of conducting wire of radius 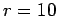 cm which
possesses
cm which
possesses 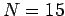 turns is placed in a uniform magnetic field. The direction
of the magnetic field makes an angle of
turns is placed in a uniform magnetic field. The direction
of the magnetic field makes an angle of  with respect to the normal
direction to the loop.
The magnetic field-strength
with respect to the normal
direction to the loop.
The magnetic field-strength 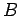 is increased at a constant
rate from
is increased at a constant
rate from 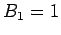 T to
T to 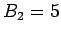 T in a time interval of
T in a time interval of
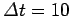 s. What
is the emf generated around the loop? If the electrical resistance of the
loop is
s. What
is the emf generated around the loop? If the electrical resistance of the
loop is 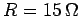 , what current flows around the loop as the
magnetic field is increased?
, what current flows around the loop as the
magnetic field is increased?
Answer: The area of the loop is
The component of the magnetic field perpendicular to the loop is
where 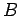 is the magnetic field-strength. Thus, the initial magnetic
flux linking the loop is
is the magnetic field-strength. Thus, the initial magnetic
flux linking the loop is
Likewise, the final flux linking the loop is
The time rate of change of the flux is
Thus, the emf generated around the loop is
Note, incidentally, that one weber per second is equivalent to one volt.
According to Ohm's law, the current which flows around the loop in response to the
emf is



Next: Worked Example 2: Lenz's
Up: Magnetic Induction
Previous: Worked Examples
Richard Fitzpatrick
2007-07-14