


Next: Power and Internal Resistance
Up: Electric Current
Previous: Capacitors in DC Circuits
Consider a simple circuit in which a battery of voltage 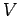 drives a
current
drives a
current 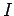 through a resistor of resistance
through a resistor of resistance 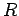 .
As we have seen, the battery is continuously doing work
by raising the potentials
of charges which flow into its negative terminal and then flow out of its
positive terminal. How much work does the battery do per unit time?
In other words, what is the power output of the battery?
.
As we have seen, the battery is continuously doing work
by raising the potentials
of charges which flow into its negative terminal and then flow out of its
positive terminal. How much work does the battery do per unit time?
In other words, what is the power output of the battery?
Consider a (positive) charge 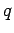 which flows through the battery from the negative
terminal to the positive terminal. The battery raises the potential of the
charge by
which flows through the battery from the negative
terminal to the positive terminal. The battery raises the potential of the
charge by 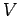 , so the work the battery does on the charge is
, so the work the battery does on the charge is 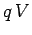 .
The total amount of charge which flows through the battery per unit time is,
by definition, equal to the current
.
The total amount of charge which flows through the battery per unit time is,
by definition, equal to the current 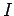 flowing through the battery. Thus, the
amount of work the battery does per unit time is simply the product of
the work done per unit
charge,
flowing through the battery. Thus, the
amount of work the battery does per unit time is simply the product of
the work done per unit
charge, 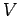 , and the charge passing through the battery per unit
time,
, and the charge passing through the battery per unit
time, 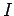 . In other words,
. In other words,
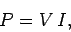 |
(141) |
where 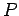 , of course, stands for the power output of the battery. Thus,
the rule is
, of course, stands for the power output of the battery. Thus,
the rule is
The power in a DC circuit is the product of the voltage and the current.
This rule does not just apply to batteries. If a current 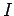 flows through
some component of a DC circuit which has a potential drop
flows through
some component of a DC circuit which has a potential drop 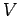 in the
direction of current flow then that component gains the energy per unit time
in the
direction of current flow then that component gains the energy per unit time
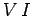 at the expense of the rest of the circuit, and vice versa.
Incidentally, since the SI unit of power is the watt (W), it follows that
at the expense of the rest of the circuit, and vice versa.
Incidentally, since the SI unit of power is the watt (W), it follows that
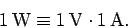 |
(142) |
Consider a resistor 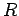 which carries a current
which carries a current 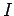 . According to Ohm's
law, the potential drop across the resistor is
. According to Ohm's
law, the potential drop across the resistor is 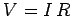 . Thus, the
energy gained by the resistor per unit time is
. Thus, the
energy gained by the resistor per unit time is
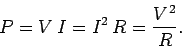 |
(143) |
In what form does the resistor acquire this energy? In turns out that
the energy is dissipated as heat inside the resistor. This effect
is known as Joule heating. Thus, the above formula
gives the electrical heating power of a resistor. Electrical energy is converted
into heat (i.e., random motion of the atoms which make up the resistor)
as the electrically accelerated free electrons inside the resistor collide with the atoms and,
thereby, transfer all of their kinetic energy to the atoms. It is this
energy which appears as heat on a macroscopic scale (see Sect. 7.3).
Household electricity bills depend on the amount of electrical
energy the household in question uses during a given accounting period,
since the energy usage determines how much coal or gas was burnt on
the household's behalf
in the local power station during this period. The conventional unit of
electrical energy usage employed
by utility companies is the kilowatthour. If electrical energy
is consumed for 1 hour at the rate of 1 kW (the typical rate of consumption of
a single-bar electric fire) then the total energy usage is
one kilowatthour (kWh). It follows that
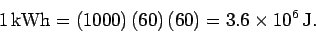 |
(144) |



Next: Power and Internal Resistance
Up: Electric Current
Previous: Capacitors in DC Circuits
Richard Fitzpatrick
2007-07-14
![]() which flows through the battery from the negative
terminal to the positive terminal. The battery raises the potential of the
charge by
which flows through the battery from the negative
terminal to the positive terminal. The battery raises the potential of the
charge by ![]() , so the work the battery does on the charge is
, so the work the battery does on the charge is ![]() .
The total amount of charge which flows through the battery per unit time is,
by definition, equal to the current
.
The total amount of charge which flows through the battery per unit time is,
by definition, equal to the current ![]() flowing through the battery. Thus, the
amount of work the battery does per unit time is simply the product of
the work done per unit
charge,
flowing through the battery. Thus, the
amount of work the battery does per unit time is simply the product of
the work done per unit
charge, ![]() , and the charge passing through the battery per unit
time,
, and the charge passing through the battery per unit
time, ![]() . In other words,
. In other words,
![]() which carries a current
which carries a current ![]() . According to Ohm's
law, the potential drop across the resistor is
. According to Ohm's
law, the potential drop across the resistor is ![]() . Thus, the
energy gained by the resistor per unit time is
. Thus, the
energy gained by the resistor per unit time is