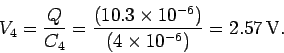

Next: Example 6.4: Energy stored
Up: Capacitance
Previous: Example 6.2: Dielectric filled
Question:
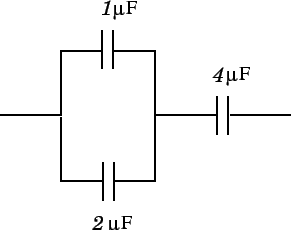
A 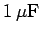 and a
and a 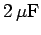 capacitor are connected in parallel, and this pair of
capacitors is then connected in series with a
capacitor are connected in parallel, and this pair of
capacitors is then connected in series with a 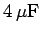 capacitor, as
shown in the diagram.
What is the equivalent capacitance of the whole combination?
What is the charge on the
capacitor, as
shown in the diagram.
What is the equivalent capacitance of the whole combination?
What is the charge on the 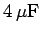 capacitor if
the whole combination is connected across the terminals of
a
capacitor if
the whole combination is connected across the terminals of
a 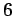 V battery? Likewise, what are the charges on the
V battery? Likewise, what are the charges on the
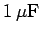 and
and 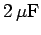 capacitors?
capacitors?
Answer: The equivalent capacitance of the 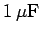 and
and 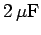 capacitors connected in parallel is
capacitors connected in parallel is
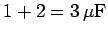 .
When a
.
When a 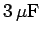 capacitor is combined in series with a
capacitor is combined in series with a
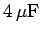 capacitor,
the equivalent capacitance of the whole combination is given by
capacitor,
the equivalent capacitance of the whole combination is given by
and so
The charge delivered by the 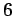 V battery is
V battery is
This is the charge on the 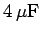 capacitor, since one of the terminals
of the battery is connected directly to one of the plates of this capacitor.
capacitor, since one of the terminals
of the battery is connected directly to one of the plates of this capacitor.
The voltage drop across the 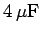 capacitor is
capacitor is
Thus, the voltage drop across the 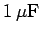 and
and 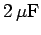 combination
must be
combination
must be
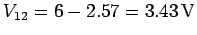 . The charge stored on the
. The charge stored on the 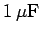 is given by
is given by
Likewise, the charge stored on the 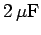 capacitor is
capacitor is
Note that the total charge stored on the 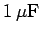 and
and 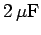 combination
is
combination
is
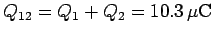 , which is the same as the charge
stored on the
, which is the same as the charge
stored on the 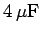 capacitor. This makes sense because the
capacitor. This makes sense because the 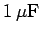 and
and 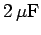 combination
and the
combination
and the 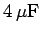 capacitor are connected in series.
capacitor are connected in series.


Next: Example 6.4: Energy stored
Up: Capacitance
Previous: Example 6.2: Dielectric filled
Richard Fitzpatrick
2007-07-14

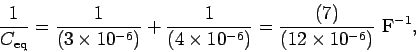
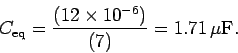
![]() V battery is
V battery is
![]() capacitor is
capacitor is