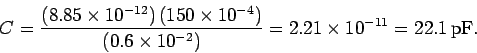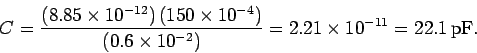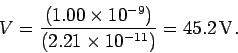Next: Example 6.2: Dielectric filled
Up: Capacitance
Previous: Worked Examples
Question: A parallel plate capacitor consists of two metal
plates, each of area
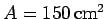 , separated by a vacuum gap
, separated by a vacuum gap
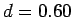 cm thick. What is the capacitance of this device? What potential
difference must be applied between the plates if the capacitor
is to hold a charge of magnitude
cm thick. What is the capacitance of this device? What potential
difference must be applied between the plates if the capacitor
is to hold a charge of magnitude
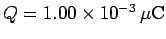 on each
plate?
on each
plate?
Solution: Making use of formula (108), the capacitance
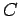 is given by
is given by
The voltage difference 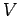 between the plates and
the magnitude of the charge
between the plates and
the magnitude of the charge 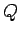 stored on each plate are related via
stored on each plate are related via
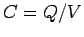 , or
, or 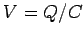 . Hence, if
. Hence, if
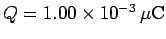 then
then
Richard Fitzpatrick
2007-07-14