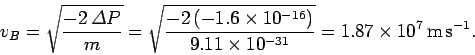Next: Example 5.3: Electric potential due
Up: Electric Potential
Previous: Example 5.1: Charge in a
Question:
An electron in a television set is accelerated from the cathode to the
screen through a potential difference of +1000 V. The screen is 35 mm from
the cathode. What is the net change in the potential energy of the electron
during the acceleration process?
How much work is done by the electric field in accelerating the
electron?
What is the speed of the electron when it strikes
the screen?
Solution: Let call the cathode point  and the screen point
and the screen point 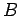 . We
are told that the potential difference between points
. We
are told that the potential difference between points 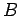 and
and  is +1000 V,
so
is +1000 V,
so
By definition, the difference in electric potential energy of some charge 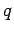 at
points
at
points 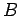 and
and  is the product of the charge and
the difference in electric potential
between these points. Thus,
is the product of the charge and
the difference in electric potential
between these points. Thus,
since
 for an electron.
Note that the potential energy of the electron decreases
as it is accelerated towards the screen. As we have seen, the electric
potential energy of a charge is actually held in the surrounding electric field.
Thus, a decrease in the potential energy of the charge corresponds to a reduction in the
energy of the field. In this case, the energy of
the field decreases because it does work
for an electron.
Note that the potential energy of the electron decreases
as it is accelerated towards the screen. As we have seen, the electric
potential energy of a charge is actually held in the surrounding electric field.
Thus, a decrease in the potential energy of the charge corresponds to a reduction in the
energy of the field. In this case, the energy of
the field decreases because it does work 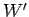 on the charge.
Clearly, the work done
(i.e., energy lost) by the field equals the decrease in potential energy
of the charge,
on the charge.
Clearly, the work done
(i.e., energy lost) by the field equals the decrease in potential energy
of the charge,
Thus,
The total energy 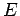 of the electron is made up of two components--the electric
potential energy
of the electron is made up of two components--the electric
potential energy 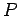 , and the kinetic energy
, and the kinetic energy 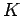 . Thus,
. Thus,
Of course,
where
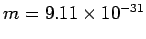 kg is the mass of the electron, and
kg is the mass of the electron, and  its speed. By conservation of energy,
its speed. By conservation of energy, 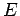 is a constant of the motion, so
is a constant of the motion, so
In other words, the decrease in electric potential energy of the electron, as
it is accelerated towards the screen, is offset by a corresponding increase in its kinetic
energy.
Assuming that the electron starts from rest (i.e. 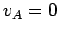 ), it follows that
), it follows that
or
Note that the distance between the cathode and the screen is immaterial in this
problem. The final speed of the electron is entirely determined by
its charge, its initial velocity,
and the potential difference through which it is accelerated.



Next: Example 5.3: Electric potential due
Up: Electric Potential
Previous: Example 5.1: Charge in a
Richard Fitzpatrick
2007-07-14
![]() of the electron is made up of two components--the electric
potential energy
of the electron is made up of two components--the electric
potential energy ![]() , and the kinetic energy
, and the kinetic energy ![]() . Thus,
. Thus,