


Next: Worked Examples
Up: Electricity
Previous: Coulomb's Law
According to Coulomb's law, a charge 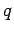 exerts a force on a second charge
exerts a force on a second charge  ,
and vice versa, even in a vacuum. But, how is this force
transmitted through empty space? In order to answer this question, physicists in the
19th Century
developed the concept of an electric field. The idea is as follows. The
charge
,
and vice versa, even in a vacuum. But, how is this force
transmitted through empty space? In order to answer this question, physicists in the
19th Century
developed the concept of an electric field. The idea is as follows. The
charge 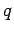 generates an electric field
generates an electric field
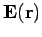 which fills space.
The electrostatic force exerted on the second charge
which fills space.
The electrostatic force exerted on the second charge  is actually produced locally by the
electric field
is actually produced locally by the
electric field  at the position of this charge, in accordance with Coulomb's law. Likewise, the charge
at the position of this charge, in accordance with Coulomb's law. Likewise, the charge  generates its
own electric field
generates its
own electric field
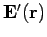 which also fills space. The equal and opposite reaction
force exerted on
which also fills space. The equal and opposite reaction
force exerted on 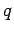 is produced locally by the electric field
is produced locally by the electric field 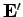 at the
position of this charge, again, in accordance with Coulomb's law. Of course, an electric field
cannot exert a force on the charge which generates it,
in just the same way as we cannot pick ourselves up with our own shoelaces. Incidentally, electric fields have a real physical existence, and are not just theoretical constructs invented by physicists to get around the
problem of the transmission of electrostatic
forces through vacuums.
We can say this with certainty because, as we shall see later, there is an energy
associated with
an electric field filling space. Indeed, it is actually possible to convert this energy into
heat or work, and vice versa.
at the
position of this charge, again, in accordance with Coulomb's law. Of course, an electric field
cannot exert a force on the charge which generates it,
in just the same way as we cannot pick ourselves up with our own shoelaces. Incidentally, electric fields have a real physical existence, and are not just theoretical constructs invented by physicists to get around the
problem of the transmission of electrostatic
forces through vacuums.
We can say this with certainty because, as we shall see later, there is an energy
associated with
an electric field filling space. Indeed, it is actually possible to convert this energy into
heat or work, and vice versa.
The electric field
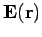 generated by a set of fixed electric charges is a vector field which is defined as follows.
If
generated by a set of fixed electric charges is a vector field which is defined as follows.
If
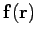 is the electrostatic force experienced by some small positive
test charge
is the electrostatic force experienced by some small positive
test charge  located at a certain point
located at a certain point 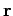 in space, then the electric field at
this point is simply the force divided by the magnitude of the test
charge. In other words,
in space, then the electric field at
this point is simply the force divided by the magnitude of the test
charge. In other words,
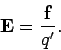 |
(62) |
Electric field has dimensions of force per unit charge, and
units of newtons per coulomb (
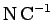 ). Incidentally, the reason
that we specify a small, rather than a large,
test charge is to avoid disturbing any of
the fixed charges
which generate the electric field.
). Incidentally, the reason
that we specify a small, rather than a large,
test charge is to avoid disturbing any of
the fixed charges
which generate the electric field.
Let us use the above rule to reconstruct the electric field generated by
a point charge 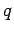 . According to Coulomb's law, the electrostatic force
exerted by a point charge
. According to Coulomb's law, the electrostatic force
exerted by a point charge 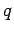 on a positive test charge
on a positive test charge  , located a distance
, located a distance
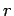 from it, has the magnitude
from it, has the magnitude
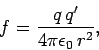 |
(63) |
and is directed radially away from the former charge if 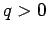 , and radially
towards it if
, and radially
towards it if 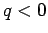 . Thus, the electric field a distance
. Thus, the electric field a distance 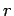 away from a charge
away from a charge 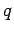 has the magnitude
has the magnitude
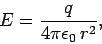 |
(64) |
and is directed radially away from the charge if 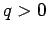 , and radially towards
the charge if
, and radially towards
the charge if 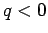 . Note that the field is independent of the magnitude
of the test charge.
. Note that the field is independent of the magnitude
of the test charge.
A corollary of the above definition of an electric field is that a stationary charge
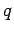 located in an electric field
located in an electric field  experiences an electrostatic force
experiences an electrostatic force
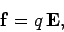 |
(65) |
where  is the electric field at the location of the charge
(excluding the field produced by the charge itself).
is the electric field at the location of the charge
(excluding the field produced by the charge itself).
Since electrostatic forces are superposable, it follows that electric fields are also superposable.
For example, if we have three stationary
point charges, 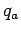 ,
, 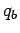 , and
, and 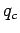 , located at three different points in space,
then the net electric field which fills space is simply the vector sum of the fields produced
by each point charge taken in isolation.
, located at three different points in space,
then the net electric field which fills space is simply the vector sum of the fields produced
by each point charge taken in isolation.



Next: Worked Examples
Up: Electricity
Previous: Coulomb's Law
Richard Fitzpatrick
2007-07-14
![]() generated by a set of fixed electric charges is a vector field which is defined as follows.
If
generated by a set of fixed electric charges is a vector field which is defined as follows.
If
![]() is the electrostatic force experienced by some small positive
test charge
is the electrostatic force experienced by some small positive
test charge ![]() located at a certain point
located at a certain point ![]() in space, then the electric field at
this point is simply the force divided by the magnitude of the test
charge. In other words,
in space, then the electric field at
this point is simply the force divided by the magnitude of the test
charge. In other words,
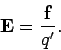
![]() . According to Coulomb's law, the electrostatic force
exerted by a point charge
. According to Coulomb's law, the electrostatic force
exerted by a point charge ![]() on a positive test charge
on a positive test charge ![]() , located a distance
, located a distance
![]() from it, has the magnitude
from it, has the magnitude
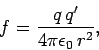
![]() located in an electric field
located in an electric field ![]() experiences an electrostatic force
experiences an electrostatic force
![]() ,
, ![]() , and
, and ![]() , located at three different points in space,
then the net electric field which fills space is simply the vector sum of the fields produced
by each point charge taken in isolation.
, located at three different points in space,
then the net electric field which fills space is simply the vector sum of the fields produced
by each point charge taken in isolation.