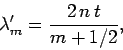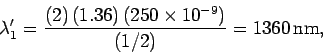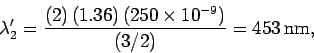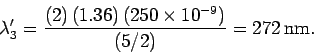Next: About this document ...
Up: Wave Optics
Previous: Example 14.1: Double slit experiment
Question: A soap bubble 250 nm thick is illuminated
by white light. The index of refraction of the soap film is  .
Which colours are not seen in the reflected light? Which colours
appear strong in the reflected light? What colour does the soap film
appear at normal incidence?
.
Which colours are not seen in the reflected light? Which colours
appear strong in the reflected light? What colour does the soap film
appear at normal incidence?
Solution: For destructive interference, we must have
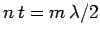 . Thus, the wavelengths that are not
reflected satisfy
. Thus, the wavelengths that are not
reflected satisfy
where
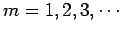 . It follows that
. It follows that
and
These are the only wavelengths close to the visible region of the
electromagnetic spectrum for which destructive interference occurs.
In fact, 680 nm lies right in the middle of the red region of the
spectrum, whilst 340 nm lies in the ultraviolet region (and is,
therefore, invisible to the human eye). It follows that the only
non-reflected colour is red.
For constructive interference, we must have
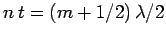 . Thus, the wavelengths that are strongly
reflected satisfy
. Thus, the wavelengths that are strongly
reflected satisfy
where
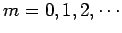 . It follows that
. It follows that
and
and
A wavelength of 272 nm lies in the ultraviolet region whereas
1360 nm lies in the infrared. Clearly, both wavelengths correspond
to light which is invisible to the human eye. The only strong reflection
occurs at 453 nm, which corresponds to the blue-violet region
of the spectrum.
The reflected light is weak in the red region of the spectrum and
strong in the blue-violet region. The soap film will, therefore, possess
a pronounced blue colour.



Next: About this document ...
Up: Wave Optics
Previous: Example 14.1: Double slit experiment
Richard Fitzpatrick
2007-07-14
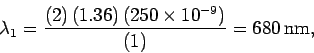
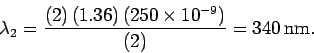
![]() . Thus, the wavelengths that are strongly
reflected satisfy
. Thus, the wavelengths that are strongly
reflected satisfy