Interference in Thin Films

In everyday life, the interference of light most commonly gives rise to easily observable effects when light impinges on a thin film of some transparent material. For instance, the brilliant colours seen in soap bubbles, in oil films floating on puddles of water, and in the feathers of a peacock's tail, are due to interference of this type.

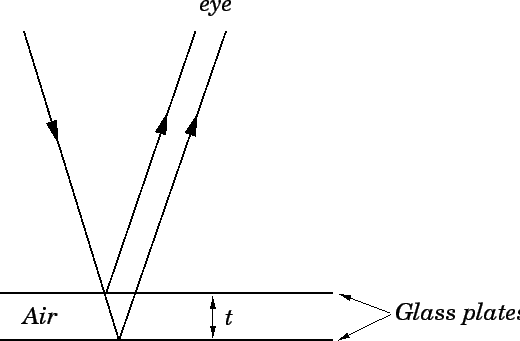
Suppose that a very thin film of air is trapped between two pieces of glass, as shown in Fig. 88. If monochromatic light (e.g., the yellow light from a sodium lamp) is incident almost normally to the film then some of the light is reflected from the interface between the bottom of the upper plate and the air, and some is reflected from the interface between the air and the top of the lower plate. The eye focuses these two parallel light beams at one spot on the retina. The two beams produce either destructive or constructive interference, depending on whether their path difference is equal to an odd or an even number of half-wavelengths, respectively.

Figure 88: Interference of light due to a thin film of air trapped between two pieces of glass.

Let $t$ be the thickness of the air film. The difference in path-lengths between the two light rays shown in the figure is clearly ${\mit\Delta}=2\,t$. Naively, we might expect that constructive interference, and, hence, brightness, would occur if ${\mit \Delta}=m\,\lambda$, where $m$ is an integer, and destructive interference, and, hence, darkness, would occur if ${\mit\Delta}=(m+1/2)\,\lambda$. However, this is not the entire picture, since an additional phase difference is introduced between the two rays on reflection. The first ray is reflected at an interface between an optically dense medium (glass), through which the ray travels, and a less dense medium (air). There is no phase change on reflection from such an interface, just as there is no phase change when a wave on a string is reflected from a free end of the string. (Both waves on strings and electromagnetic waves are transverse waves, and, therefore, have analogous properties.) The second ray is reflected at an interface between an optically less dense medium (air), through which the ray travels, and a dense medium (glass). There is a $180^\circ$ phase change on reflection from such an interface, just as there is a $180^\circ$ phase change when a wave on a string is reflected from a fixed end. Thus, an additional $180^\circ$ phase change is introduced between the two rays, which is equivalent to an additional path difference of $\lambda/2$. When this additional phase change is taken into account, the condition for constructive interference becomes

$$2\,t=(m+1/2)\,\lambda,$$ (377)

where $m$ is an integer. Similarly, the condition for destructive interference becomes

$$2\,t = m\,\lambda.$$ (378)

For white light, the above criteria yield constructive interference for some wavelengths, and destructive interference for others. Thus, the light reflected back from the film exhibits those colours for which the constructive interference occurs.

If the thin film consists of water, oil, or some other transparent material of refractive index $n$ then the results are basically the same as those for an air film, except that the wavelength of the light in the film is reduced from $\lambda$ (the vacuum wavelength) to $\lambda/n$. It follows that the modified criteria for constructive and destructive interference are

$$2\,n\,t=(m+1/2)\,\lambda,$$ (379)

and

$$2\,n\,t = m\,\lambda,$$ (380)

respectively.