


Next: Huygens' principle
Up: Wave Optics
Previous: Wave Optics
Introduction
Geometric optics is an incredibly successful theory. Probably its
most important application is in describing and explaining
the operation of
commonly occurring optical instruments: e.g., the camera, the telescope, and the microscope.
Although geometric optics does not make any explicit assumption about
the nature of light, it tends to suggest that light consists of a
stream of massless particles. This is certainly what scientists, including,
most notably, Isaac Newton,
generally assumed up until about the year 1800.
Let us examine how the particle theory of light accounts for the three basic
laws of geometric optics:
- The law of geometric propagation: This is easy. Massless
particles obviously move in straight-lines in free space.
- The law of reflection: This is also fairly easy. We merely
have to assume that light particles bounce elastically
(i.e., without energy loss) off reflecting surfaces.
- The law of refraction: This is the tricky one. Let us
assume that the speed of light particles propagating through a transparent
dielectric medium is proportional to the
index of refraction,
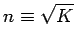 .
Let us further assume that at a general
interface between two different dielectric
media, light particles crossing the interface conserve
momentum in the plane parallel to the interface. In general, this implies
that the particle momenta normal to the interface are not conserved:
i.e., the interface exerts a normal reaction force on crossing
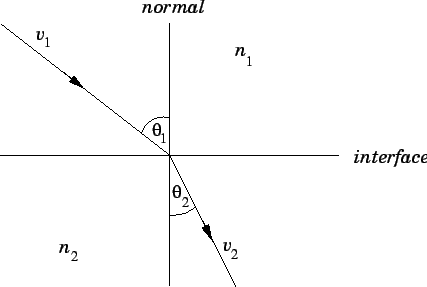
particles, but no parallel force. From Fig. 83,
parallel momentum conservation for light particles crossing the interface
yields
.
Let us further assume that at a general
interface between two different dielectric
media, light particles crossing the interface conserve
momentum in the plane parallel to the interface. In general, this implies
that the particle momenta normal to the interface are not conserved:
i.e., the interface exerts a normal reaction force on crossing
particles, but no parallel force. From Fig. 83,
parallel momentum conservation for light particles crossing the interface
yields
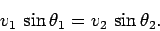 |
(368) |
However, by assumption, 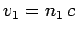 and
and 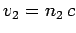 , so
, so
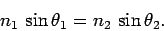 |
(369) |
This highly contrived (and incorrect) derivation of the law of refraction
was first proposed by Descartes in 1637. Note that it depends
crucially on the (incorrect) assumption that light travels
faster in dense media (e.g., glass)
than in rarefied media (e.g., water). This assumption
appears very strange to us nowadays, but it seemed eminently reasonable
to scientists in the 17th and 18th centuries. After all, they knew that
sound travels faster in dense media (e.g., water) than in rarefied
media (e.g., air).
Figure 83:
Descartes' model of refraction
 |
The wave theory of light, which became established in the first
half of the 19th century, initially encountered tremendous resistance.
Let us briefly
examine the reasons why scientists in the early 1800s refused
to think of light as a wave phenomenon? Firstly, the particle theory of
light was intimately associated with Isaac Newton, so any attack on this
theory was considered to be a slight to his memory. Secondly, all of the
waves that scientists were familiar with at that time manifestly
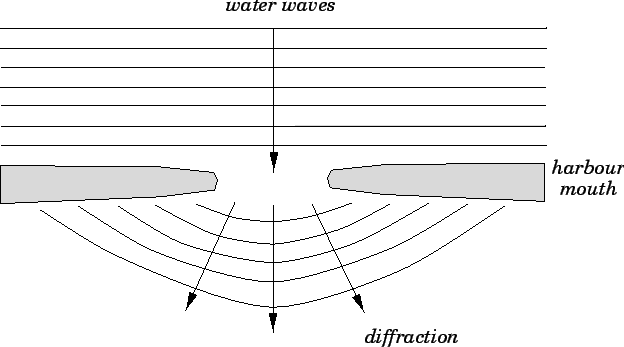
did not travel in straight-lines. For instance, water waves are
diffracted as they pass through the narrow mouth of a harbour, as shown
in Fig. 84. In other words, the ``rays'' associated with such waves
are bent as they traverse the harbour mouth.
Scientists thought that if light were a wave phenomenon then it would also not
travel in straight-lines: i.e., it would not cast straight, sharp
shadows, any more than water waves cast straight, sharp ``shadows.''
Unfortunately, they did not appreciate that if the wavelength of light
is much shorter than that of water waves then light can be a wave
phenomenon and still propagate in a largely geometric manner.
Figure 84:
Refraction of water waves through the entrance of a harbour.
 |



Next: Huygens' principle
Up: Wave Optics
Previous: Wave Optics
Richard Fitzpatrick
2007-07-14