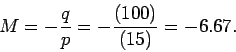Next: Example 13.2: Convex mirrors
Up: Paraxial Optics
Previous: Worked Examples
Question: An object of height 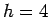 cm is placed
a distance
cm is placed
a distance 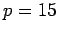 cm in front of a concave mirror of
focal length
cm in front of a concave mirror of
focal length 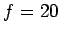 cm. What is the height, location, and
nature of the image? Suppose that the object is
moved to a new position a distance
cm. What is the height, location, and
nature of the image? Suppose that the object is
moved to a new position a distance  cm in front
of the mirror. What now is the height, location, and
nature of the image?
cm in front
of the mirror. What now is the height, location, and
nature of the image?
Answer: According to Eq. (358), the image distance 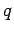 is
given by
is
given by
Thus, the image is virtual (since 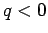 ), and is located
), and is located 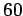 cm behind
the mirror. According to Eq. (352), the magnification
cm behind
the mirror. According to Eq. (352), the magnification  of
the image is given by
of
the image is given by
Thus, the image is upright (since 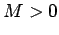 ), and
magnified by a factor of
), and
magnified by a factor of 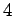 . It follows that the height
. It follows that the height
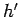 of
the image is given by
of
the image is given by
If the object is moved such that 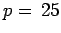 cm then the
new image distance is given by
cm then the
new image distance is given by
Thus, the new image is real (since 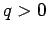 ), and is
located 100cm in front of the mirror. The new magnification is
given by
), and is
located 100cm in front of the mirror. The new magnification is
given by
Thus, the image is inverted (since 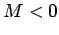 ), and
magnified by a factor of
), and
magnified by a factor of  . It follows that the
new height of the image
is
. It follows that the
new height of the image
is
Note that the height is negative because the image is inverted.



Next: Example 13.2: Convex mirrors
Up: Paraxial Optics
Previous: Worked Examples
Richard Fitzpatrick
2007-07-14
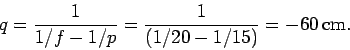
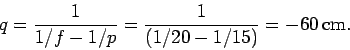
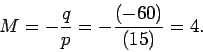
![]() cm then the
new image distance is given by
cm then the
new image distance is given by