


Next: Thin Lenses
Up: Paraxial Optics
Previous: Image Formation by Convex
Both concave and convex spherical mirrors asymptote to plane mirrors
in the limit in which their radii of curvature 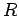 tend to infinity.
In other words, a plane mirror can be treated as either
a concave or a convex mirror
for which
tend to infinity.
In other words, a plane mirror can be treated as either
a concave or a convex mirror
for which
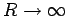 . Now, if
. Now, if
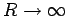 , then
, then
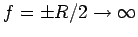 , so
, so
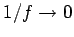 , and Eq. (358)
yields
, and Eq. (358)
yields
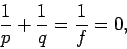 |
(359) |
or
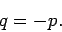 |
(360) |
Thus, for a plane mirror the image is virtual, and is
located as far behind the mirror as the object is in front of
the mirror. According to Eq. (352), the magnification of the
image is given by
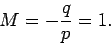 |
(361) |
Clearly, the image is upright, since 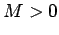 , and is
the same size
as the object, since
, and is
the same size
as the object, since 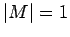 . However, an image seen
in a plane mirror does differ from the original object in one
important respect: i.e.,
left and right are swapped over. In other words,
a right-hand looks like a left-hand in a plane mirror, and vice
versa.
. However, an image seen
in a plane mirror does differ from the original object in one
important respect: i.e.,
left and right are swapped over. In other words,
a right-hand looks like a left-hand in a plane mirror, and vice
versa.



Next: Thin Lenses
Up: Paraxial Optics
Previous: Image Formation by Convex
Richard Fitzpatrick
2007-07-14