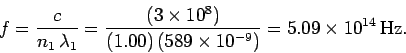Next: Paraxial Optics
Up: Geometric Optics
Previous: Example 12.1: The corner-cube
Question: A light-ray of wavelength
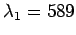 nm
traveling through air is incident on a smooth, flat slab of
crown glass (refractive index 1.52) at an angle of
nm
traveling through air is incident on a smooth, flat slab of
crown glass (refractive index 1.52) at an angle of
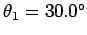 to the normal. What is the angle of refraction?
What is the wavelength
to the normal. What is the angle of refraction?
What is the wavelength 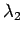 of the light inside the glass?
What is the frequency
of the light inside the glass?
What is the frequency 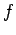 of the light inside the glass?
of the light inside the glass?
Answer: Snell's law can be written
In this case,
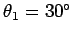 ,
,
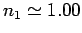 (here, we neglect the
slight deviation of the refractive index of air from that of a
vacuum), and
(here, we neglect the
slight deviation of the refractive index of air from that of a
vacuum), and 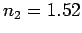 . Thus,
. Thus,
giving
as the angle of refraction (measured with respect to the normal).
The wavelength 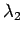 of the light inside the glass is given by
of the light inside the glass is given by
The frequency  of the light inside the glass is exactly the same
as the frequency outside the glass, and is given by
of the light inside the glass is exactly the same
as the frequency outside the glass, and is given by



Next: Paraxial Optics
Up: Geometric Optics
Previous: Example 12.1: The corner-cube
Richard Fitzpatrick
2007-07-14
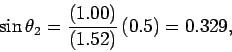
![]() of the light inside the glass is given by
of the light inside the glass is given by
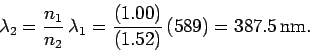
![]() of the light inside the glass is exactly the same
as the frequency outside the glass, and is given by
of the light inside the glass is exactly the same
as the frequency outside the glass, and is given by