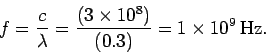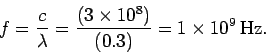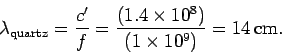Next: Example 11.2: Intensity of
Up: Electromagnetic Waves
Previous: Worked Examples
Question: Consider electromagnetic waves of wavelength
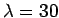 cm in air. What is the frequency of such waves? If such waves pass
from air into a block of quartz, for which
cm in air. What is the frequency of such waves? If such waves pass
from air into a block of quartz, for which 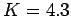 , what is their new
speed, frequency, and wavelength?
, what is their new
speed, frequency, and wavelength?
Answer: Since, 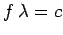 , assuming that the dielectric constant of air is approximately unity, it follows that
, assuming that the dielectric constant of air is approximately unity, it follows that
The new speed of the waves as they pass propagate through the
quartz is
The frequency of electromagnetic waves does not change when the medium through
which the waves are propagating changes. Since 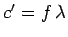 for
electromagnetic waves propagating through a dielectric medium, we have
for
electromagnetic waves propagating through a dielectric medium, we have
Richard Fitzpatrick
2007-07-14