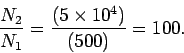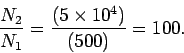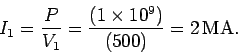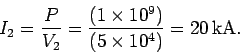Next: Example 10.6: Impedance matching
Up: Inductance
Previous: Example 10.4: The RC
Question: An electric power plant produces 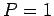 GW of AC
electric power at a peak voltage of
GW of AC
electric power at a peak voltage of 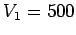 V. If it is desired to
transmit this power at a peak voltage of
V. If it is desired to
transmit this power at a peak voltage of 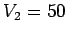 kV,
what is the appropriate turns-ratio of the step-up transformer?
What peak current
kV,
what is the appropriate turns-ratio of the step-up transformer?
What peak current 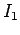 would be sent over the transmission line if the peak
voltage were
would be sent over the transmission line if the peak
voltage were 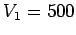 V? What peak current
V? What peak current 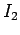 would be sent over the transmission
line if the peak
voltage were
would be sent over the transmission
line if the peak
voltage were 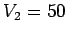 kV? What is the ratio of the ohmic powers losses in
the line in the two cases?
kV? What is the ratio of the ohmic powers losses in
the line in the two cases?
Answer: The appropriate turns-ratio
is
Since the peak power is given by 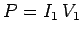 , it follows that
, it follows that
Since the peak power remains unchanged after the signal
passes through the transformer (assuming that there are no
power losses in the transformer), we have
The ratio of the power lost to ohmic heating in the two
cases is
where 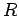 is the resistance of the transmission line. Note that the ohmic
power loss is much greater at low peak voltage than at high peak voltage.
is the resistance of the transmission line. Note that the ohmic
power loss is much greater at low peak voltage than at high peak voltage.



Next: Example 10.6: Impedance matching
Up: Inductance
Previous: Example 10.4: The RC
Richard Fitzpatrick
2007-07-14