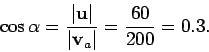Next: Newton's laws of motion
Up: Motion in 3 dimensions
Previous: Worked example 3.4: Hail
Question: United Airlines flight UA589 from Chicago is 20miles due
North of Austin's Bergstrom airport. Suppose that the plane is flying
at
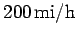 relative to the air. Suppose, further, that there
is a wind blowing due East at
relative to the air. Suppose, further, that there
is a wind blowing due East at
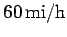 . Towards which compass bearing must
the plane steer in order to land at the airport?
. Towards which compass bearing must
the plane steer in order to land at the airport?
Answer: The problem in hand is illustrated in the diagram.
The plane's velocity 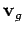 relative to the ground is the
vector sum of its velocity
relative to the ground is the
vector sum of its velocity 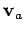 relative to the air, and the
velocity
relative to the air, and the
velocity 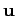 of the wind relative to the ground. We know that
of the wind relative to the ground. We know that
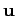 is directed due East, and we require
is directed due East, and we require 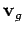 to be directed
due South. We also know that
to be directed
due South. We also know that
 and
and
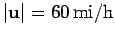 .
Now, from simple trigonometry,
.
Now, from simple trigonometry,
Hence,
However, it is clear from the diagram that the compass bearing 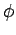 of the
plane is given by
of the
plane is given by
Thus, in order to land at Bergstrom airport the plane must fly towards compass
bearing 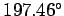 .
.



Next: Newton's laws of motion
Up: Motion in 3 dimensions
Previous: Worked example 3.4: Hail
Richard Fitzpatrick
2006-02-02