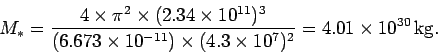Next: Worked example 12.6: Launch
Up: Orbital motion
Previous: Worked example 12.4: Halley's
Question: A planet is in circular orbit around a star. The
period and radius of the orbit are
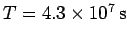 and
and
 ,
respectively. Calculate the mass of the star.
,
respectively. Calculate the mass of the star.
Answer: Let  be the planet's orbital angular velocity. The
planet accelerates towards the star with acceleration
be the planet's orbital angular velocity. The
planet accelerates towards the star with acceleration 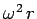 . The acceleration
due to the star's gravitational attraction is
. The acceleration
due to the star's gravitational attraction is 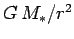 , where
, where 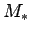 is the
mass of the star. Equating these accelerations, we obtain
is the
mass of the star. Equating these accelerations, we obtain
Now,
Hence,
combining the previous two expressions, we get
Thus, the mass of the star is
Richard Fitzpatrick
2006-02-02
![]() be the planet's orbital angular velocity. The
planet accelerates towards the star with acceleration
be the planet's orbital angular velocity. The
planet accelerates towards the star with acceleration ![]() . The acceleration
due to the star's gravitational attraction is
. The acceleration
due to the star's gravitational attraction is ![]() , where
, where ![]() is the
mass of the star. Equating these accelerations, we obtain
is the
mass of the star. Equating these accelerations, we obtain