


Next: Worked example 11.2: Block
Up: Oscillatory motion
Previous: Uniform circular motion
Question: A piston in a stream engine executes simple harmonic motion.
Given that the maximum displacement of the piston from its centre-line is
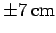 ,
and that the mass of the piston is
,
and that the mass of the piston is 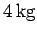 , find the maximum velocity of the piston
when the steam engine is running at 4000rev./min. What is the maximum acceleration?
, find the maximum velocity of the piston
when the steam engine is running at 4000rev./min. What is the maximum acceleration?
Answer: We are told that the amplitude of the oscillation is
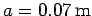 .
Moreover, when converted to cycles per second (i.e., hertz), the frequency of the oscillation becomes
.
Moreover, when converted to cycles per second (i.e., hertz), the frequency of the oscillation becomes
Hence, the angular frequency is
Consulting Tab. 4, we note that the maximum velocity of an object executing
simple harmonic motion is
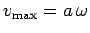 . Hence, the maximum velocity is
. Hence, the maximum velocity is
Likewise, according to Tab. 4, the maximum acceleration is given by



Next: Worked example 11.2: Block
Up: Oscillatory motion
Previous: Uniform circular motion
Richard Fitzpatrick
2006-02-02
![]() .
Moreover, when converted to cycles per second (i.e., hertz), the frequency of the oscillation becomes
.
Moreover, when converted to cycles per second (i.e., hertz), the frequency of the oscillation becomes