


Next: Velocity
Up: Motion in 1 dimension
Previous: Introduction
Consider a body moving in 1 dimension: e.g., a train traveling down a straight
railroad track, or a truck driving down an interstate in Kansas. Suppose that we have
a team of observers who continually report the location of this body to us as time
progresses. To be more exact, our observers report the distance  of the body
from
some arbitrarily chosen reference point located on the track on which it is constrained to move. This
point is known as the origin of our coordinate system. A positive
of the body
from
some arbitrarily chosen reference point located on the track on which it is constrained to move. This
point is known as the origin of our coordinate system. A positive  value implies
that the body is located
value implies
that the body is located  meters to the right of the origin, whereas a negative
meters to the right of the origin, whereas a negative
 value implies that the body is located
value implies that the body is located  meters to the left of the origin.
Here,
meters to the left of the origin.
Here,  is termed the displacement of the body from the origin. See Fig. 2.
Of course, if the body is extended then our observers will have to report the displacement
is termed the displacement of the body from the origin. See Fig. 2.
Of course, if the body is extended then our observers will have to report the displacement
 of some conveniently chosen reference point on the body (e.g., its centre
of mass) from the origin.
of some conveniently chosen reference point on the body (e.g., its centre
of mass) from the origin.
Our information regarding the body's motion consists of a set of data points,
each specifying the displacement  of the body at some time
of the body at some time  . It is
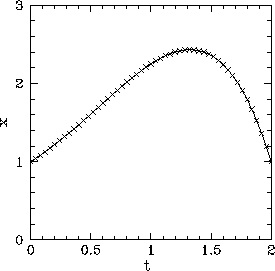
usually illuminating to graph these points. Figure 3 shows an example of such a graph.
As is often the case, it is possible to fit the data points appearing in this
graph using a relatively
simple analytic curve. Indeed, the curve associated with Fig. 3 is
. It is
usually illuminating to graph these points. Figure 3 shows an example of such a graph.
As is often the case, it is possible to fit the data points appearing in this
graph using a relatively
simple analytic curve. Indeed, the curve associated with Fig. 3 is
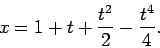 |
(11) |
Figure 2:
Motion in 1 dimension
 |
Figure 3:
Graph of displacement versus time
 |



Next: Velocity
Up: Motion in 1 dimension
Previous: Introduction
Richard Fitzpatrick
2006-02-02
![]() of the body at some time
of the body at some time ![]() . It is
usually illuminating to graph these points. Figure 3 shows an example of such a graph.
As is often the case, it is possible to fit the data points appearing in this
graph using a relatively
simple analytic curve. Indeed, the curve associated with Fig. 3 is
. It is
usually illuminating to graph these points. Figure 3 shows an example of such a graph.
As is often the case, it is possible to fit the data points appearing in this
graph using a relatively
simple analytic curve. Indeed, the curve associated with Fig. 3 is