


Next: Statics
Up: Angular momentum
Previous: Worked example 9.2: Angular
Question: A skater spins at an initial angular velocity of
 with her arms outstretched. The skater then lowers her arms, thereby
decreasing her moment of inertia by a factor
with her arms outstretched. The skater then lowers her arms, thereby
decreasing her moment of inertia by a factor 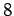 . What is the skater's final
angular velocity? Assume that any friction between the skater's skates and the
ice is negligible.
. What is the skater's final
angular velocity? Assume that any friction between the skater's skates and the
ice is negligible.
Answer: Neglecting any friction between the skates and the ice, we
expect the skater to spin with constant angular momentum. The skater's initial
angular momentum is
where 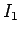 is the skater's initial moment of inertia. The skater's final angular
momentum is
is the skater's initial moment of inertia. The skater's final angular
momentum is
where 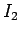 is the skater's final moment of inertia, and
is the skater's final moment of inertia, and 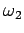 is her final
angular velocity. Conservation of angular momentum yields
is her final
angular velocity. Conservation of angular momentum yields 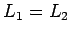 , or
, or
Now, we are told that  . Hence,
. Hence,
Richard Fitzpatrick
2006-02-02