Next: Angular momentum
Up: Rotational motion
Previous: Worked example 8.6: Horsepower
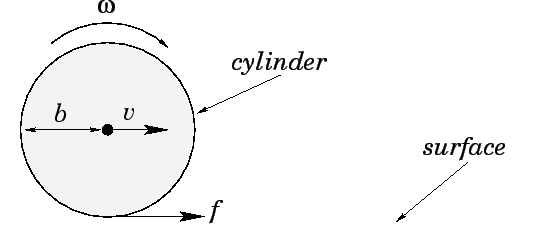
Question: A uniform cylinder of radius
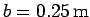 is given
an angular speed of
is given
an angular speed of
 about an axis, parallel
to its length, which passes through its centre. The cylinder is gently lowered onto
a horizontal frictional surface, and released. The coefficient of friction
of the surface is
about an axis, parallel
to its length, which passes through its centre. The cylinder is gently lowered onto
a horizontal frictional surface, and released. The coefficient of friction
of the surface is  . How long does it take before the
cylinder starts to roll without slipping? What distance does the cylinder
travel between its release point and the point at which it commences to
roll without slipping?
. How long does it take before the
cylinder starts to roll without slipping? What distance does the cylinder
travel between its release point and the point at which it commences to
roll without slipping?
Answer: Let  be the velocity of the cylinder's centre of mass,
be the velocity of the cylinder's centre of mass,
 the cylinder's angular velocity,
the cylinder's angular velocity, 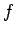 the frictional force exerted by the
surface on the cylinder,
the frictional force exerted by the
surface on the cylinder,  the cylinder's mass, and
the cylinder's mass, and 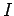 the cylinder's moment of inertia.
The cylinder's translational equation of motion is written
the cylinder's moment of inertia.
The cylinder's translational equation of motion is written
Note that the friction force acts to accelerate the cylinder's translational motion.
Likewise, the cylinder's rotational equation of motion takes the form
since the perpendicular distance between the line of action of 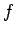 and the axis
of rotation is the radius,
and the axis
of rotation is the radius, 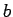 , of the cylinder.
Note that the friction force acts to decelerate the cylinder's rotational
motion.
If the cylinder is slipping with respect to the surface, then the friction force,
, of the cylinder.
Note that the friction force acts to decelerate the cylinder's rotational
motion.
If the cylinder is slipping with respect to the surface, then the friction force,
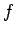 , is equal to the coefficient of friction,
, is equal to the coefficient of friction,  , times the normal reaction,
, times the normal reaction,
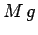 , at the surface:
, at the surface:
Finally, the moment of inertia of the cylinder is
The above equations can be solved to give
Given that  (i.e., the cylinder
is initially at rest) and
(i.e., the cylinder
is initially at rest) and
 at time
at time  , the above
expressions can be integrated to give
, the above
expressions can be integrated to give
which yields
Now, the cylinder stops slipping as soon as the ``no slip'' condition,
is satisfied. This occurs when
Whilst it is slipping, the cylinder travels a distance



Next: Angular momentum
Up: Rotational motion
Previous: Worked example 8.6: Horsepower
Richard Fitzpatrick
2006-02-02

![]() be the velocity of the cylinder's centre of mass,
be the velocity of the cylinder's centre of mass,
![]() the cylinder's angular velocity,
the cylinder's angular velocity, ![]() the frictional force exerted by the
surface on the cylinder,
the frictional force exerted by the
surface on the cylinder, ![]() the cylinder's mass, and
the cylinder's mass, and ![]() the cylinder's moment of inertia.
The cylinder's translational equation of motion is written
the cylinder's moment of inertia.
The cylinder's translational equation of motion is written