


Next: Worked example 8.6: Horsepower
Up: Rotational motion
Previous: Worked example 8.4: Weight
Question: A uniform rod of mass
 and length
and length
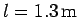 rotates about a fixed frictionless pivot located at one of its ends. The rod is released from
rest at an angle
rotates about a fixed frictionless pivot located at one of its ends. The rod is released from
rest at an angle
 beneath the horizontal. What is the angular acceleration
of the rod immediately after it is released?
beneath the horizontal. What is the angular acceleration
of the rod immediately after it is released?
Answer: The moment of inertia of a rod of mass  and length
and length 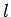 about
an axis, perpendicular to its length, which passes through one of its ends is
about
an axis, perpendicular to its length, which passes through one of its ends is
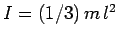 (see question 8.3). Hence,
(see question 8.3). Hence,
The angular equation of motion of the rod is
where 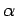 is the rod's angular acceleration, and
is the rod's angular acceleration, and 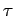 is the net torque exerted on the
rod. Now, the only force acting on the rod (whose line of action does not pass through
the pivot) is the rod's weight,
is the net torque exerted on the
rod. Now, the only force acting on the rod (whose line of action does not pass through
the pivot) is the rod's weight,  . This force acts at the centre of mass of the rod,
which is situated at the rod's midpoint. The perpendicular distance
. This force acts at the centre of mass of the rod,
which is situated at the rod's midpoint. The perpendicular distance  between the
line of action of the weight and the pivot point is simply
between the
line of action of the weight and the pivot point is simply
Thus, the torque acting on the rod is
It follows that the rod's angular acceleration is written



Next: Worked example 8.6: Horsepower
Up: Rotational motion
Previous: Worked example 8.4: Weight
Richard Fitzpatrick
2006-02-02


![]() and length
and length ![]() about
an axis, perpendicular to its length, which passes through one of its ends is
about
an axis, perpendicular to its length, which passes through one of its ends is
![]() (see question 8.3). Hence,
(see question 8.3). Hence,