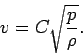Next: Motion in 1 dimension
Up: Introduction
Previous: Worked example 1.2: Tire
Question: The speed of sound  in a gas might plausibly depend on
the pressure
in a gas might plausibly depend on
the pressure  , the density
, the density 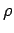 , and the volume
, and the volume 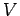 of the gas. Use
dimensional analysis to determine the exponents
of the gas. Use
dimensional analysis to determine the exponents  ,
,  , and
, and  in the
formula
in the
formula
where  is a dimensionless constant. Incidentally, the mks units
of pressure are kilograms per meter per second squared.
is a dimensionless constant. Incidentally, the mks units
of pressure are kilograms per meter per second squared.
Answer: Equating the dimensions of both sides of the above equation, we
obtain
A comparison of the exponents of ![$[L]$](img76.png) ,
, ![$[M]$](img77.png) , and
, and ![$[T]$](img78.png) on either side of the
above expression yields
on either side of the
above expression yields
The third equation immediately gives 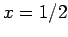 ; the second equation then yields
; the second equation then yields 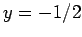 ; finally,
the first equation gives
; finally,
the first equation gives 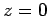 . Hence,
. Hence,



Next: Motion in 1 dimension
Up: Introduction
Previous: Worked example 1.2: Tire
Richard Fitzpatrick
2006-02-02
![\begin{displaymath}
\frac{[L]}{[T]} = \left(\frac{[M]}{[T^2][L]}\right)^x\left(
\frac{[M]}{[L^3]}\right)^y [L^3]^z.
\end{displaymath}](img106.png)