

Next: Determination of Ecliptic Latitude
Up: Planetary Latitudes
Previous: Jupiter
The ecliptic latitude of Saturn can be determined with the aid of Tables 54, 71, and 72. Table 54 allows
the mean argument of latitude, 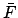 , of Saturn to be calculated as a function of
time. Next, Table 71 permits the deferential latitude,
, of Saturn to be calculated as a function of
time. Next, Table 71 permits the deferential latitude, 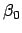 , to
be determined as a function of the true argument of latitude,
, to
be determined as a function of the true argument of latitude, 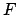 . Finally, Table 72 allows the quantities
. Finally, Table 72 allows the quantities
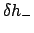 ,
, 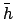 , and
, and 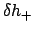 to be calculated as functions of the epicyclic
anomaly,
to be calculated as functions of the epicyclic
anomaly, 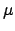 . The procedure for using these tables is analogous to the previously described procedure for
using the Mars tables.
One example of this procedure is given below.
. The procedure for using these tables is analogous to the previously described procedure for
using the Mars tables.
One example of this procedure is given below.
Example: May 5, 2005 CE, 00:00 UT:
From Cha. 8,
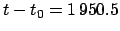 JD,
JD,
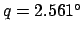 ,
,
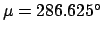 ,
,
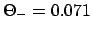 , and
, and
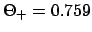 .
Making use of
Table 54, we find:
.
Making use of
Table 54, we find:
| |
|
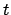 (JD) (JD) |
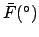 |
| |
|
| +1000 |
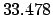 |
| +900 |
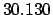 |
| +50 |
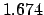 |
| +.5 |
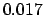 |
| Epoch |
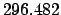 |
| |
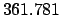 |
| Modulus |
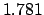 |
| |
|
Thus,
It follows from Table 71 that
Since
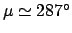 , Table 72 yields
, Table 72 yields
so
Finally,
Thus,
the ecliptic latitude of Saturn at 00:00 UT on May 5, 2005 CE was 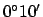 .
.


Next: Determination of Ecliptic Latitude
Up: Planetary Latitudes
Previous: Jupiter
Richard Fitzpatrick
2010-07-21
![]() JD,
JD,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
Making use of
Table 54, we find:
.
Making use of
Table 54, we find: